Букет кіл

Буке́т кіл (відомий також як роза) — топологічний простір, отриманий склеюванням набору кіл навколо однієї точки. Кола букета іноді називають пелюстками троянди. Букети кіл важливі в алгебричній топології, де вони тісно пов'язані з вільними групами.

Букет чотирьох кіл (роза з чотирма пелюстками)

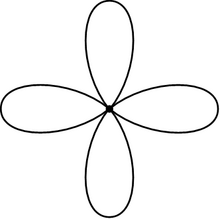
Визначення

Фундаментальна група вісімки є вільною групою, згенерованою елементами a та b

Букет кіл є окремим випадком букета просторів. Тобто букет кіл є фактор-простором C/S, де C — незв'язне об'єднання кіл за множиною S, яка складається по одній точці з кожного кола. Як клітинний комплекс букет кіл має одну вершину і по одному ребру для кожного кола. Це робить його простим прикладом топологічного графа.

Букет із n кіл можна отримати також ототожненням n точок одного кола. Букет із двох кіл називають вісімкою.

Зв'язок із вільними групами

Універсальне накриття вісімки можна візуалізувати графом Келі вільної групи на двох генераторах a та b

Фундаментальна група букета кіл є вільною з одним генератором для кожної пелюстки. Універсальне накриття є нескінченним деревом, яке можна ототожнити з графом Келі вільної групи. (Це окремий випадок комплексу задань, асоційованого з будь-яким заданням групи.)

Проміжні накриття букета кіл відповідають підгрупам вільної групи. Спостереження, що будь-яке накриття букета кіл є графом, дає просте доведення, що будь-яка підгрупа вільної групи вільна (теорема Нільсена — Шреєра).

Оскільки універсальне накриття букета кіл стягується, букет кіл є K(F,1) простором для асоційованої вільної групи F . З цього випливає, що когомологія груп $H^{n}(F)$ тривіальна для $n\geqslant 2$.

Інші властивості

Вісімка в тор

• Будь-який зв'язний граф гомотопічно еквівалентний букету кіл. Зокрема, букет кіл є фактор-простором графа, отриманого стягуванням кістякового дерева.
• Куля з видаленими n точками (або сфера з видаленими $n+1$ точками) є деформаційним ретрактом у букет кіл з n пелюстками. Одне з кіл букета оточує кожну з видалених точок.
• Тор з однією видаленою точкою є деформаційним ретрактом у вісімку, а саме об'єднання двох породжувальних кіл. Загальніше, поверхня роду g з однією видаленою точкою є деформаційним ретрактом у букет кіл з 2g пелюстками, а саме в межу фундаментального многокутника.
• Букет кіл може мати нескінченно багато пелюсток, що приводить до фундаментальної групи, яка вільна на нескінченно великій кількості генераторів. Букет зі зліченного кіл подібний до гавайської сережки — є неперервна бієкція з букета кіл у гавайську сережку, але вони не гомеоморфні.

Див. також

• Букет (граф)
• Квадрифолій (чотирилисник)
• Вільна група
• Топологічний граф

Література

• Allen Hatcher. Algebraic topology. — Cambridge, UK : Cambridge University Press, 2002. — ISBN 0-521-79540-0.
• James R. Munkres. Topology. — Englewood Cliffs, N.J : Prentice Hall, Inc, 2000. — ISBN 0-13-181629-2.
• John Stillwell. Classical topology and combinatorial group theory. — Berlin : Springer-Verlag, 1993. — ISBN 0-387-97970-0.