Портал:Математика/Архів вибраних статей
Фрактал
 |
| Границя множини Мандельброта. |
Фракта́л (лат. fractus — подрібнений, дробовий) – нерегулярна, самоподібна структура. В широкому розумінні фрактал означає фігуру, малі частини якої в довільному збільшенні є подібними до неї самої. Термін фрактал було введено в 1975 році Бенуа Мандельбротом.
Об'єкти, які тепер називаються фракталами, досліджувались задовго до того, як їм було дано таку назву. В етноматематиці, наприклад в роботах Рона Еглаша "Африканські Фрактали", (ISBN 0-8135-2613-2) задокументовано поширені фрактальні геометричні фігури в мистецтві тубільців. В 1525 році німецький митець Альбрехт Дюрер опублікував свою працю Керівництво Художника, один із розділів якої має назву "Черепичні шаблони, утворені пентагонами". Пентагон Дюрера багато в чому є схожим на килим Серпінського, але замість квадратів використовуються п'ятикутники. Джексон Поллок (американський експресіоніст 50-тих років) малював об'єкти, дуже схожі на фрактали.
Порівняно простий клас прикладів становлять множини Кантора, в яких короткі та ще коротші (відкриті) інтервали вилучаються з одиничного інтервалу [0; 1], залишаючи множину, яка, можливо, буде (або не буде) самоподібною при збільшенні. Також до прикладів фракталів належить фрактал Ляпунова, трикутник Серпінського, килим Серпінського, губка Менгера, крива дракона, крива заповнення простору, межі множин груп Кліні та крива Коха. Фрактали можуть бути детермінованими або стохастичними (наприклад, недетермінованими).
Приблизні фрактали можна легко знайти в природі. Ці об'єкти мають самоподібну структуру при великих, але обмежених діапазонах збільшень. Як приклади можна назвати хмари, сніжинки, гори, мережі річок, та системи кровоносних судин.
| Переглянути всі | Далі... |
Квантова механіка
 |
| Густини ймовірності, що відповідають хвильовим функціям електрона атома водню. |
Ква́нтова меха́ніка — фундаментальна фізична теорія, що в описі мікроскопічних об'єктів розширює, уточнює і поєднує результати класичної механіки і класичної електродинаміки. Ця теорія є базою для багатьох напрямів фізики та хімії, включаючи фізику твердого тіла, квантову хімію та фізику елементарних частинок. Термін «квантова» (від лат. quantum — «скільки») пов'язаний з дискретними порціями, які теорія присвоює певним фізичним величинам, наприклад, енергії електромагнітної хвилі.
Механіка — наука, що описує рух тіл і співставлені йому фізичні величини, такі як енергія чи імпульс. Розвиток класичної механіки призвів до значних успіхів у розумінні навколишнього світу, однак вона має свої обмеження. Квантова механіка дає точніші і більш правдиві результати для багатьох явищ. Це стосується як явищ мікроскопічного масштабу (тут класична механіка не здатна пояснити навіть існування стабільного атома), так і деяких макроскопічних явищ, таких як надпровідність, надплинність чи випромінювання абсолютно чорного тіла. Уже впродовж століття існування квантової механіки її передбачення ніколи не були заперечені експериментом. Квантова механіка пояснює принаймні три типи явищ, якиx класична механіка та класична електродинаміка не може описати.
| Переглянути всі | Далі... |
Алгоритм
 |
| Сторінка з «Алгебри» аль-Хорезмі. |
Алгор́итм (латинізов. Algorithmi, від імені перського математика IX ст. аль-Хорезмі) — послідовність, система, набір систематизованих правил виконання обчислювального процесу, що обов'язково приводить до розв'язання певного класу задач після скінченного числа операцій. При написанні комп'ютерних програм алгоритм описує логічну послідовність операцій. Для візуального зображення алгоритмів часто використовують блок-схеми.
Кожен алгоритм є списком добре визначених інструкцій для розв'язання задачі. Починаючи з початкового стану, інструкції алгоритму описують процес обчислення, які відбуваються через послідовність станів, які, зрештою, завершуються кінцевим станом. Перехід з одного стану до наступного не обов'язково детермінований — деякі алгоритми містять елементи випадковості.
Поняття алгоритму належить до первісних, основних, базисних понять математики, таких, як множина чи натуральне число. Обчислювальні процеси алгоритмічного характеру (арифметичні дії над цілими числами, знаходження найбільшого спільного дільника двох чисел тощо) відомі людству з глибокої давнини. Проте, в явному вигляді поняття алгоритму сформувалося лише на початку XX століття.
| Переглянути всі | Далі... |
Полярна система координат
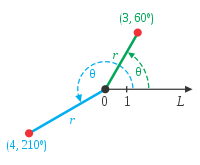 |
| Точки в полярній системі координат. |
Полярна система координат — двовимірна система координат, в якій кожна точка на площині визначається двома числами — кутом та відстанню. Полярна система координат особливо корисна у випадках, коли відношення між точками найпростіше зобразити у вигляді відстаней та кутів; в більш поширеній, Декартовій, або прямокутній системі координат, такі відношення можна встановити лише шляхом застосування тригонометричних рівнянь.
Полярна система координат задається променем, який називають нульовим або полярною віссю. Точка, з якої виходить цей промінь називається початком координат або полюсом. Будь-яка інша точка на площині визначається двома полярними координатами: радіальною та кутовою. Радіальна координата (зазвичай позначається ) відповідає відстані від точки до початку координат. Кутова координата, що також зветься полярним кутом або азимутом і позначається φ, дорівнює куту, на який потрібно повернути проти годинникової стрілки полярну вісь для того, щоб потрапити в цю точку.
Визначена таким чином радіальна координата може приймати значення від нуля до нескінченості, а кутова координата змінюється в межах від 0° до 360°. Однак, для зручності область значень полярної координати можна розширити за межі повного кута, а також дозволити їй приймати від'ємні значення, що відповідатиме повороту полярної осі за годинниковою стрілкою.
| Переглянути всі | Далі... |
Теорема Піфагора
 |
| Вавилонська табличка Plimpton 322. |
Історію теореми Піфагора можна розділити на чотири частини: знання про Піфагорові числа, знання про відношення сторін в прямокутному трикутнику, знання про відношення суміжних кутів та доведення теореми.
Мегалітичні споруди близько 2500 до н. е. в Єгипті та Північній Європі містять прямокутні трикутники із сторонами з цілих чисел. Бартель ван дер Варден висловив гіпотезу, що в ті часи Піфагорові числа були знайдені алгебраїчно.
Написаний між 2000 та 1876 до н. е. папірус часів Середнього Єгипетського царства Berlin 6619 містить задачу, розв'язком якої є числа Піфагора.
Написана під час правління Хамурапі Великого (між 1790 і 1750 до н.е) вавилонська табличка Plimpton 322 містить багато записів, тісно пов'язаних із числами Піфагора.
В сутрах Будхаяни, які датуються за різними версіями 8-им чи 2-им століттям до н. е. в Індії, містить Піфагорові числа виведені алгебраїчно, формулювання теореми Піфагора та геометричне доведення для рівнобедренного прямокутного трикутника.
| Переглянути всі | Далі... |
Архімед
 |
| Задумливий Архімед, Доменіко Фетті. |
Архімед (дав.-гр. ᾽Αρχιμήδης; близько 287 до н. е., Сіракузи — 212 до н. е., Сіракузи) — давньогрецький математик, фізик, інженер, винахідник та астроном. Хоча дуже мало деталей відомо про його життя, він вважається одним з найвидатніших науковців античності. Серед його досягнень у фізиці, — заснування гідростатики, статики та пояснення принципу важеля. Йому приписують винайдення новаторських механізмів, включно з осадними машинами та гвинтовим насосом, що названий на його честь. Сучасними експериментами перевіряли твердження, що Архімедові машини могли піднімати кораблі в повітря та підпалювати їх за допомогою набору дзеркал.
Архімед, як правило, вважається найвидатнішим математиком античності та одним з найвидатніших всіх часів. Він використовував метод вичерпування, щоб розрахувати площу обмежену дугою параболи шляхом розрахунку суми нескінченного ряду і дав надзвичайно точне наближення числа пі. Він також винайшов спіраль, що носить його ім’я, формули для розрахунку об’ємів поверхонь обертання та оригінальну систему для вираження дуже великих чисел.
Архімед помер під час облоги Сіракуз, вбитий римським солдатом, попри виданий наказ не заподіювати йому шкоди. Цицерон описує свій візит на могилу Архімеда, яку увінчувала сфера вписана в циліндр. Архімед довів, що сфера має дві треті від площі та об'єму описаного циліндра (включно з його основами) і вважав це одним з своїх найбільших математичних досягнень.
| Переглянути всі | Далі... |
Фізика
 |
| Синхротрон. Сучасна фізика використовує гігантські експериментальні інструменти. |
Фі́зика (від грец. φυσικός природний, φύσις природа) — природнича наука, яка досліджує загальні властивості матерії та явищ у ній, а також виявляє загальні закони, які керують цими явищами; це наука про закономірності Природи в широкому сенсі цього слова. Фізики вивчають поведінку та властивості матерії в широких межах її проявів, від субмікроскопічних елементарних частинок, з яких побудоване все матеріальне (фізика елементарних частинок), до поведінки всього Всесвіту, як єдиної системи (космологія).
Деякі з закономірностей, які встановлені фізикою, є загальними для всіх матеріальних систем. До таких можна віднести, наприклад, закон збереження енергії. Такі закономірності називають законами фізики. Фізику вважають фундаментальною наукою, тому що всі інші природничі науки (хімія, геологія, біологія, тощо) мають справу з певними різновидами матеріальних систем, які підкоряються законам фізики. Наприклад, властивості хімічних речовин визначаються властивостями молекул та атомів, які їх складають, а ці властивості досліджують в таких галузях фізики, як квантова механіка, термодинаміка і/або електрика (електромагнетизм).
Фізика також тісно пов'язана з математикою. Фізичні теорії, як правило, побудовані на основі певного математичного апарату і цей апарат часто набагато складніший в порівнянні з іншими природничими науками.
| Переглянути всі | Далі... |
Трикутник Рело
 |
| Mappa mundi. Леонардо да Вінчі, приблизно 1514 рік. |
Трику́тник Рело́ — плоска опукла геометрична фігура, найпростіша після кола фігура сталої ширини. Утворюється перетином трьох однакових кіл з радіусом і центрами, розміщеними у вершинах рівностороннього трикутника зі стороною , де — число, яке називають шириною отриманої фігури.
Сталість цієї ширини означає наступне: якщо до трикутника Рело провести пару паралельних опорних прямих, то відстань між ними завжди буде рівною , незалежно від обраного напрямку. Одна з цих прямих завжди проходить через одну з вершин трикутника, а друга є дотичною до протилежної дуги
Трикутник Рело обмежує негладка замкнута опукла крива, яка носить таку ж назву. Вона походить від прізвища німецького механіка Франца Рело, який першим продемонстрував сталість ширини цієї фігури і використовував її у своїх механізмах.
Серед інших фігур сталої ширини трикутник Рело виділяє низка його граничних властивостей — найменша площа, найменший можливий кут при вершині, найбільша асиметричність щодо центру. Також трикутник набув поширення в техніці — на його основі були створені кулачкові та грейферні механізми, роторний двигун Ванкеля, і навіть дрилі, що дозволяють свердлити квадратні отвори.
| Переглянути всі | Далі... |
Рівняння четвертого степеня
 |
| Джироламо Кардано. |
Рівняння четвертого степеня було вперше розглянуто математиками Індії між 400 до н. е. і 200 н. е.
Лодовіко Феррарі першим відкрив розв'язок рівнянь четвертого степеня (1540), проте його робота мала один недолік: він спирався на розв'язок кубічного рівняння, яким він не володів, тому цей розв'язок не було опубліковано. Цей розв'язок було опублікувано разом із розв'язком кубічного рівняння його наставником Джироламо Кардано у книзі «Ars Magna» (1545).
Розв'язок рівнянь вищих степенів (від п'ятого) у загальному випадку не можна подати в радикалах. Але недоведеність цього факту протягом деякого часу підбурювала вчених шукати такі розв'язки. 1824 року було опубліковано теорему Абеля-Руффіні, яка доводила неможливість подати корені рівнянь вищих степенів через радикали у загальному випадку.
| Переглянути всі | Далі... |

