Довжина хвилі
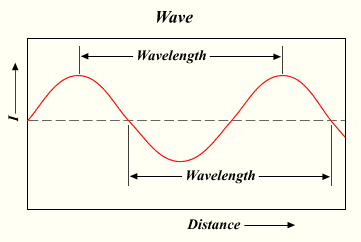
Довжина́ хви́лі — характеристика періодичної хвилі, що позначає найменшу відстань між точками простору, в яких хвиля має однакову фазу[1]. Крива на представленому малюнку може розглядатися, наприклад, як миттєвий знімок збурень у струні, коли відхилення точок струни від стану рівноваги задається виразом
- .
Тут , де — фазова швидкість хвилі, а — кругова частота.
Довжина хвилі зазвичай позначається грецькою літерою λ. Ця характеристика хвилі однозначно зв'язана з величиною хвильового числа k
- .
Порівняння двох виразів для хвильового числа вказує на залежність довжини хвилі від частоти. Для згаданого випадку хвиль в струні фазова швидкість є постійною величиною. Тому в струні хвилі різних частот (довжин хвиль) поширюються з однаковою швидкістю. В багатьох випадках при вивченні хвиль їхня фазова швидкість виявляється залежною від частоти. Це явище називають дисперсією. Співвідношення, що задає зв'язок між фазовою швидкістю і частотою називається законом дисперсії, або дисперсійним рівнянням.
Часто залежність між частотою і довжиною хвилі обернено-пропорційна. У таких випадках швидкість розповсюдження хвилі фіксована й не залежить від частоти. Наприклад, для електромагнітної хвилі у вакуумі
де c — швидкість світла.
Аналогічно, для звукових хвиль
де s — швидкість звуку.
При переході хвилі з одного середовища в інше довжина хвилі змінюється, на відміну від частоти, яка залишається сталою. Електромагнітні хвилі в середовищі зазвичай характеризуються приведеною довжиною хвилі, тобто довжиною, яку хвиля мала б у вакуумі.
Синусоїдні хвилі ред.
В лінійному[en] середовищі, будь-яку форму хвилі можна описати в термінах незалежного поширення синусоїдних компонентів. Довжина хвилі λ синусоїдної хвилі, що рухається із постійною швидкістю v задається як[2]
де v це величина фазової швидкості) хвилі, а f це її частота. В дисперсивному середовищі, фазова швидкість залежить від частоти хвилі, що робить зв'язок між довжиною хвилі і частотою нелінійним.
У випадку з Електромагнітним випромінюванням — таким як світло — у вільному просторі, фазова швидкість дорівнює швидкості світла, що є близькою 3×108 м/сек. Таким чином довжина хвилі 100 МГц електромагнітної (радіо) хвилі становить близько: 3×108 м/сек розділене на 108 Гц = 3 метри. Довжина хвиль видимого світла варіюється від темно червоного, що має довжину хвилі приблизно в 700 нм, до фіолетового, приблизно 400 нм (інші приклади див. електромагнітний спектр).
Для звукових хвиль в повітрі, Швидкість звуку становить 343 м/сек (в при нормальних умовах температури і атмосферного тиску). Людський слух може сприймати довжини хвиль звукових частот (20 Гц–20 кГц) будуть знаходитися в межах приблизно від 17 м до 17 мм, відповідно. Зверніть увагу, що довжини хвиль чутного звуку набагато довші за довжини хвиль видимого світла.
Стояча хвиля ред.
Стояча хвиля це хвилеподібний рух, який залишається на одному місці. Синусоїдальна стояча хвиля має стаціонарні точки, де рух не відбувається, які називаються вузлами[en], а довжина хвилі вдвічі більша за відстань між вузлами.
На верхньому малюнку показано три стоячі хвилі у коробці. Стінки коробки зроблені так, що хвиля повинна мати вузли на стінках цієї коробки (приклад крайових умов), це визначає які довжини хвиль потрібні. Наприклад, для електромагнітної хвилі, якщо коробка має ідеальні металеві стінки, умови для появи вузлів на стінках виникають тому що металеві стінки не можуть підтримувати тангенціальне електричне поле, що приводить до того, що хвиля має нульову амплітуду на стінках.
Стаціонарну хвилю можна розглядати як суму двох синусоїдних хвиль, що поширюються із протилежно направленими швидкостями.[3] Таким чином, довжина хвилі, період і швидкість хвилі пов'язані так само як і для біжучої хвилі. Наприклад, швидкість світла можна визначити за допомогою спостереження за стоячими хвилями в металевій коробці в якій знаходиться ідеальний вакуум.
Математичне представлення ред.
Рухомі синусоїдні хвилі часто задають математично через їх швидкість v (в напрямі осі x), частоту f і довжину хвилі λ наступним чином:
де y це значення хвилі в будь-якій точці позиції x, при часі t, і A задає амплітуду хвилі. Також, їх часто задають в термінах хвильового числа k (кількість довжин хвилі, що поміщаються в 2π одиниць довжини) і кутової частоти ω (2π помножене на частоту) як:
де довжина хвилі і хвильове число пов'язані до швидкості і частоти наступним чином:
або
У другому виразі рівняння, що наведене вище, фаза (kx − ωt) часто узагальнена до виразу (k•r − ωt), що замінює хвильове число k на хвильовий вектор, який задає напрям та хвильове число для плоскої хвилі у тривимірному просторі, параметризоване за допомогою вектора позиції r. В такому випадку, хвильове число k, магнітуда k, досі залишаються у тому самому співвідношенні із довжиною хвилі як було показаному вище, де v інтерпретують як скалярну швидкість, напрям якої задає хвильовий вектор. Перша форма в якій використовується відповідна довжина хвилі в фазі, не так легко узагальнюється до задавання хвилі в довільному напрямку.
Також використовують узагальнення до синусоїд з іншими фазами, а також до комплексних експонент; див плоска хвиля. Загальноприйняте використання косинусної фази замість синусної фази при описанні хвилі основане на тому, що косинус є дійсною частиною комплексної експоненти для хвилі
Загальне середовище ред.
Швидкість хвилі залежить від середовища в якому вона поширюється. Зокрема, швидкість світла в середовищі є меншою ніж у вакуумі, це означає, що та сама частота буде відповідати меншій довжині хвилі у середовищі, ніж у вакуумі, як показано на малюнку праворуч.
Ця зміна швидкості при входженні в середовище призводить до заломлення, тобто до зміни напрямку руху хвиль, які зустрічають перехід між середовищами під кутом.[4] Для електромагнітних хвиль, ця зміна кута поширення описується законом Снеліуса.
Не тільки швидкість хвилі в одному середовищі, може відрізнятися від швидкості в іншому середовищі, а швидкість як правило змінюється із довжиною хвилі. В результаті, зміна напряму при вході в інше середовище відбувається зі зміною довжини хвилі.
Для електромагнітних хвиль швидкість поширення у середовищі визначається його показником заломлення відповідно до
де c це швидкість світла у вакуумі, а n(λ0) це показник заломлення середовища для довжини хвилі λ0, де остання вимірюється у вакуумі, а не в середовищі. Відповідна довжина хвилі у середовищі становить
Якщо вказують довжини хвиль електромагнітного випромінення, як правило вказують значення довжини хвилі у вакуумі, якщо явно не визначено, що це довжина хвилі у певному середовищі. В акустиці, де середовище є необхідним для існування хвиль, довжина хвилі вказується для відповідного зазначеного середовища.
Зміна швидкості світла із довжиною хвилі називається дисперсією, це явище також можна спостерігати при проходженні світла через призму[en], коли світло розділяється на складові кольори. Розділення на кольори відбувається коли показник заломлення в середині призми змінюється для різної довжини хвилі, тож хвилі із різною довжиною в середині призми поширюються із різною швидкістю, що змушує їх заломлюватися під різними кутами. Математичний закон, який описує як швидкість світла в середовищі змінюється із його довжиною хвилі відомий як закон дисперсії.
Неоднорідне середовище ред.
Довжина хвилі може бути корисним поняттям, навіть якщо хвиля не періодична у просторі. Наприклад, океанські хвилі, які наближуються до берега, показані на малюнку, мають різну локальну довжину хвилі, яка частково залежить від глибини морського дна у співвідношенні до висоти хвилі. Аналіз цих хвиль може засновуватися на порівнянні локальної довжини хвилі із локальною глибиною води.[5]
Хвилі, синусоїдні у часі, але поширювані через середовище, властивості якого змінюються із положенням у ньому (неоднорідне середовище), можуть поширюватися зі швидкістю, яка також буде змінюватися із положенням, і таким чином не будуть синусоїдними у просторі. Приклад показано на малюнку праворуч. З тим як хвиля сповільнюється, довжина хвилі стає меншою, а амплітуда зростає; після проходження місця максимального відгуку, короткі хвилі викликають високі втрати і зрештою хвиля згасає.
Аналіз диференційних рівнянь, що описують такі системи часто проводять наближеними методами, такими як метод наближення ВКБ (що також відомий як метод Ліувілля–Гріна). Метод інтегрує фазу у просторі рішення, що є функцією часу і простору, використовуючи локальне хвильове число, яке можна розуміти як відповідник «локальної довжини хвилі».[6][7] Цей метод розглядає систему локально, так ніби вона є однорідною із деякими локальними властивостями; зокрема, локальна швидкість хвилі пов'язана із частотою є єдиною необхідною інформацією для оцінки відповідного хвильового числа або довжини хвилі. Крим того, метод обчислює повільну зміну амплітуди аби узгодити інші обмеження рівнянь фізичної системи, такі як для визначення збереження енергії у хвилі.
Кристали ред.
Хвилі в кристалічних твердих тілах не є неперервними, оскільки вони утворені вібрацією дискретних частинок, що організовані у регулярні решітки. Це створює аліасинг, оскільки одна і та однакову вібрацію, можна розглядати як таку, що має різні довжини хвиль, як показано на малюнку.[8] Описувати це використовуючи більше ніж одну із цих частот було б надмірним; як правило обирають найдовшу довжину хвилі що відповідає цьому явищу. Діапазон довжин хвиль, якого достатньо аби надати опис усіх можливих хвиль в кристалічному середовищі відповідає векторам хвилі, що прив'язані до зони Бріллюена.[9]
Ця невизначеність довжини хвилі у твердих тілах є важливою для аналізу хвильових явищ, таких як енергетичні смуги та коливання решітки. Математично це еквівалентне аліасингу сигналу, який представлено у дискретних інтервалах.
Загальні форми хвиль ред.
Поняття довжини хвилі як правило застосовують до синусоїдних, або близьких до синусоїдних, хвиль, оскільки в лінійній системі синусоїда це унікальна форма, яка поширюється без зміни форми — змінюється лише фаза і потенційно змінюється амплітуда.[10] Довжина хвилі (альтернативно хвильове число або хвильовий вектор) є характеристикою хвилі в просторі, яка функціонально пов'язана із частотою хвилі. Синусоїди є найпростішим варіантом біжучих хвиль, а складніші варіанти хвиль можна побудувати за допомогою суперпозиції.
Особливому випадку бездисперсійних і однорідних середовищ, хвилі відмінні від синусоїдних поширюються із незмінною формою та сталою швидкістю. В певних обставинах, хвилі із незмінною формою можуть зустрічатися у нелінійних середовищах; наприклад, на малюнку показані океанські хвилі на мілководді, які мають більш чіткі гребні і більш пологий прогин ніж у синусоїди, що є типовим для кноїдальних хвиль[en],[11] біжучі хвилі, які описуються за допомогою еліптичних функцій Якобі m-го прядку, що як правило позначаються як cn(x; m).[12] Океанічні хвилі з великою амплітудою певних форм можуть поширюватися без змін, завдяки властивостям нелінійності середовища поверхневих хвиль.[13]
Якщо біжуча хвиля має фіксовану форму, яка повторюється в просторі або з часом, це періодична хвиля.[14] Такі хвилі як правило вважають таким, що мають довжину хвилі, хоча вони не є синусоїдними.[15] Як показано на малюнку, довжина хвилі вимірюється між послідовними відповідними точками форми хвилі.
Хвильовий пакет ред.
Локалізовані хвильові пакети, «сплески» хвиль, коли кожний пакет хвиль рухається як одне ціле, знайшли застосування у багатьох областях фізики. Хвильовий пакет має огинаючу, що описує загальну амплітуду хвилі; між огинаючою, відстань між сусідніми піками іноді називають локальною довжиною хвилі.[16][17] Приклад показаний на малюнку. В загальному випадку, контур хвильового пакету рухається із відмінною швидкістю ніж складові хвилі.[18]
Якщо використати Аналіз Фур'є, хвильові пакети можна аналізувати у вигляді нескінченної суми (або інтегралу) синусоїдних хвиль із різним хвильовим числом або довжиною хвилі.[19]
Луї де Бройль стверджував, що всі частинки із певним значенням імпульсу p мають довжину хвилі λ = h/p, де h це Стала Планка. Ця гіпотеза лягла в основу квантової механіки. У сучасний час, ці хвилі називаються хвилями де Бройля. Наприклад, електрони у дисплеях із електронно-променевою трубкою мають довжину хвилі де Бройля, що приблизно дорівнює 10−13 м. Аби уникнути того, що хвильова функція, що описує таку частинку буде поширюватися по всьому простору, Бройль запропонував використовувати хвильові пакети, аби представити частинку, яка локалізована у просторі.[20] Поширення хвильового пакета у просторі, і розподіл хвильових чисел синусоїд, що утворюють пакет, відповідатиме невизначеності позиції частинки і імпульсу, добуток яких обмежено принципом невизначеності.[19]
Інтерференція та дифракція ред.
Інтерференція для двох щілин ред.
Коли хвилі синусоїдної форми складаються між собою, вони можуть посилити одна одну (конструктивна інтерференція) або погасити одна одну (деструктивна інтерференція) в залежності від їх взаємного співвідношення фаз. Це явище можна дослідити за допомогою інтерферометра. Це простий експеримент який здійснив Томас Юнг, в якому світло проходить через дві щілини.[21] Як показано на малюнку, світло проходить крізь щілини і відбиває світло на екрані. Шлях, який проходить світло до певної точки на екрані буде різним для кожної із щілин, і залежить від значення кута θ, який траєкторії цих шляхів утворюють з екраном. Якщо ми розмістили екран досить далеко від щілин (так що, s є великою відстанню відносно відстані d, на яку рознесені щілини), тоді ці шляхи будуть приблизно паралельними, і різниця шляхів буде просто дорівнювати d sin θ. Відповідно, умова для конструктивної інтерференції буде наступною:[22]
де m це ціле число, а умова для деструктивної інтерференції буде наступна:
Таким чином, якщо відома довжина хвилі даного світла, рознесення щілин можна визначити із утвореного візерунка або смужок, і навпаки.
Для декількох щілин, візерунок буде наступним[23]
де q задає кількість щілин, а g — стала дифракційної ґратки. Перший фактор, I1, є результатом для однієї щілини.
Дифракція із однією щілиною ред.
Поняття різниці шляхів і конструктивної та деструктивної інтерференції описані вище для умови з двома щілинами застосовується також і для дослідження світла, що проходить крізь одну щілину і відбиває слід на екрані. Основним результатом цієї інтерференції є розподілення світла через вузьку щілину у більш широке зображення на екрані. Це розсіяне розподілення енергії хвилі називають дифракцією.
В залежності від відстані між джерелом та екраном, розрізняють два типи дифракції: Дифракцію Фраунгофера або дифракція із далеким полем при великому віднесенні і Дифракцію Френеля або дифракцію близького поля і близькому віднесенні.
При аналізі дифракції із однією щілиною враховують не нульову ширину щілини, а кожну точку апертури приймають за джерело, що має єдиний вплив на пучок світла (вейвлети Гюйгенса). На екрані, світло, що проходить шлях від кожної точки в щілині має різну довжину шляху, хоча й дуже невелику різницю. Отже, як наслідок, виникає інтерференція.
У дифракційному візерунку Фраунгофера, досить далеко віднесеного від щілини, застосовуючи малокутове наближення, розподілення інтенсивності S співвідноситься із позицією x через квадрат функції sinc:[24]
- де
де L це ширина щілини, R це відстань від отриманого візерунка (на екрані) до щілини, а λ довжина хвилі застосованого світла. Функція S має нулі, там де u це не нульове ціле число, і при тих значеннях x, із довжиною хвилі в пропорції із відстанню віднесення.
Обмеження роздільної здатності дифракції ред.
Дифракція є основним обмеженням роздільної здатності оптичних інструментів, таких як телескопи (в тому числі радіотелескопів) та мікроскопи.[25] Для кругової апертури, точка зображення обмежена дифракцією відома як диск Ейрі; відстань x в формулі дифракції з однією щілиною заміняються радіальною відстанню r, а синус заміняється на 2J1, де J1 — функція Бесселя першого порядку.[26]
Просторовий розмір об'єкті, які можливо розрізнити при спостереженні за допомогою мікроскопа обмежений критерієм Релея, тобто співвідношенням радіуса першого затемнення диску Ейрі, до розміру пропорційному довжині хвилі світла, яке використовується і залежить від числової апертури[en]:[27]
де числова апертура визначена як для кута θ, який є половиною кута конуса променів, що приймаються об'єктивом мікроскопа.
Кутовий розмір центральної яскравої ділянки (радіус до першого затемнення диску Ейрі) зображення, що зазнала дії дифракції кругової апертури, є мірою, яку як правило використовують для телескопів та камер, і дорівнює:[28]
де λ це довжина хвилі для тих хвиль які необхідно зобразити, D це діаметр вхідної зіниці системи зображення, що вказується в тих самих одиницях, і кутова роздільна здатність δ в радіанах.
Як і інші дифракційні візерунки, цей візерунок масштабується в залежності від довжини хвилі, тож менша довжина хвилі дозволяє мати вищу роздільну здатність.
Субхвильова довжина ред.
Термін субхвильова довжина (англ. subwavelength) використовується для опису об'єкта, який взаємодіє із хвилею, і має розмір в один або декілька вимірів менший ніж довжина хвилі. Наприклад, термін оптичне волокно із діаметром субхвильової довжини[en] означає оптоволокно, діаметр якого менший ніж довжина хвилі світла, що проходить по ньому.
Субхвильовою частинкою є частинка, яка менша ніж довжина хвилі світла з яким вона взаємодіє (див. Релеївське розсіювання світла). Субхвильова апертура, це отвір менший ніж довжина хвилі світла, який проходить через нього. Такі конструкції мають своє застосування у надзвичайній оптичній передачі[en], і світловодах нульового режиму[en], серед усіх інших областей фототоніки.
Субхвильова довжина може також означати явище пов'язане із субхвильовими об'єктами; наприклад, візуалізацією субхвильової довжини[en].
Кутова довжина хвилі ред.
Величина, що пов'язана із довжиною хвилі — кутова довжина хвилі (що також відома як зменшена довжина хвилі), як правило позначається як ƛ (лямбда із рисочкою). Вона дорівнює «повній» довжині хвилі, що «зменшена» на коефіцієнт 2π (ƛ = λ/2π). Вона як правило зустрічається в квантовій механіці, де використовується у поєднанні із скороченою сталою Планка (позначається ħ) і кутовою частотою (позначається символом ω) або кутовим хвильовим числом (символ k).
Див. також ред.
Примітки ред.
- ↑ ДСТУ 2755-94 Фізична оптика. Терміни, визначення та літерні позначення основних величин.
- ↑ David C. Cassidy; Gerald James Holton; Floyd James Rutherford (2002). Understanding physics. Birkhäuser. с. 339 ff. ISBN 0-387-98756-8. Архів оригіналу за 8 лютого 2017. Процитовано 5 лютого 2019.
- ↑ John Avison (1999). The World of Physics. Nelson Thornes. с. 460. ISBN 978-0-17-438733-6. Архів оригіналу за 12 лютого 2020. Процитовано 6 лютого 2019.
- ↑ Raymond T. Pierrehumbert (2010). Principles of Planetary Climate. Cambridge University Press. с. 327. ISBN 0-521-86556-5. Архів оригіналу за 10 лютого 2020. Процитовано 9 лютого 2019.
- ↑ а б Paul R Pinet (2009). op. cit. с. 242. ISBN 0-7637-5993-7. Архів оригіналу за 9 лютого 2020. Процитовано 9 лютого 2019.
- ↑ Bishwanath Chakraborty (2007). Principles of Plasma Mechanics. New Age International. с. 454. ISBN 978-81-224-1446-2. Архів оригіналу за 11 лютого 2020. Процитовано 9 лютого 2019.
- ↑ Jeffrey A. Hogan & Joseph D. Lakey (2005). Time-frequency and time-scale methods: adaptive decompositions, uncertainty principles, and sampling. Birkhäuser. с. 348. ISBN 978-0-8176-4276-1. Архів оригіналу за 24 січня 2020. Процитовано 9 лютого 2019.
- ↑ See Figure 4.20 in A. Putnis (1992). Introduction to mineral sciences. Cambridge University Press. с. 97. ISBN 0-521-42947-1. Архів оригіналу за 11 лютого 2020. Процитовано 9 лютого 2019. and Figure 2.3 in Martin T. Dove (1993). Introduction to lattice dynamics (вид. 4th). Cambridge University Press. с. 22. ISBN 0-521-39293-4. Архів оригіналу за 14 лютого 2020. Процитовано 9 лютого 2019.
- ↑ Manijeh Razeghi (2006). Fundamentals of solid state engineering (вид. 2nd). Birkhäuser. с. 165 ff. ISBN 0-387-28152-5. Архів оригіналу за 11 лютого 2020. Процитовано 9 лютого 2019.
- ↑ See Lord Rayleigh (1890). Wave theory. Encyclopædia Britannica (вид. 9th). The Henry G Allen Company. с. 422.
- ↑ Valery N. Pilipchuk (2010). Figure 4.4: Transition from quasi-harmonic to cnoidal wave. Nonlinear Dynamics: Between Linear and Impact Limits. Springer. с. 127. ISBN 3642127983. Архів оригіналу за 13 лютого 2020. Процитовано 10 лютого 2019.
- ↑ Andrei Ludu (2012). §18.3 Special functions. Nonlinear Waves and Solitons on Contours and Closed Surfaces (вид. 2nd). Springer. с. 469 ff. ISBN 3642228941. Архів оригіналу за 14 лютого 2020. Процитовано 10 лютого 2019.
- ↑ Alfred Osborne (2010). Chapter 1: Brief history and overview of nonlinear water waves. Nonlinear Ocean Waves and the Inverse Scattering Transform. Academic Press. с. 3 ff. ISBN 0-12-528629-5. Архів оригіналу за 13 лютого 2020. Процитовано 10 лютого 2019.
- ↑ Alexander McPherson (2009). Waves and their properties. Introduction to Macromolecular Crystallography (вид. 2). Wiley. с. 77. ISBN 0-470-18590-2. Архів оригіналу за 3 лютого 2020. Процитовано 10 лютого 2019.
- ↑ Eric Stade (2011). Fourier Analysis. John Wiley & Sons. с. 1. ISBN 1-118-16551-9. Архів оригіналу за 12 лютого 2020. Процитовано 10 лютого 2019.
- ↑ Peter R. Holland (1995). The Quantum Theory of Motion: An Account of the de Broglie–Bohm Causal Interpretation of Quantum Mechanics. Cambridge University Press. с. 160. ISBN 978-0-521-48543-2. Архів оригіналу за 26 січня 2020. Процитовано 15 лютого 2019.
- ↑ Jeffery Cooper (1998). Introduction to partial differential equations with MATLAB. Springer. с. 272. ISBN 0-8176-3967-5. Архів оригіналу за 15 лютого 2020. Процитовано 15 лютого 2019.
The local wavelength λ of a dispersing wave is twice the distance between two successive zeros. ... the local wavelength and the local wave number k are related by k = 2π / λ.
- ↑ A. T. Fromhold (1991). Wave packet solutions. Quantum Mechanics for Applied Physics and Engineering (вид. Reprint of Academic Press 1981). Courier Dover Publications. с. 59 ff. ISBN 0-486-66741-3. Архів оригіналу за 31 січня 2020. Процитовано 15 лютого 2019.
(p. 61) ... the individual waves move more slowly than the packet and therefore pass back through the packet as it advances
- ↑ а б See, for example, Figs. 2.8–2.10 in Joy Manners (2000). Heisenberg's uncertainty principle. Quantum Physics: An Introduction. CRC Press. с. 53—56. ISBN 978-0-7503-0720-8. Архів оригіналу за 7 квітня 2021. Процитовано 15 лютого 2019.
- ↑ Ming Chiang Li (1980). Electron Interference. У L. Marton; Claire Marton (ред.). Advances in Electronics and Electron Physics. Т. 53. Academic Press. с. 271. ISBN 0-12-014653-3. Архів оригіналу за 17 лютого 2020. Процитовано 15 лютого 2019.
- ↑ Greenfield Sluder & David E. Wolf (2007). IV. Young's Experiment: Two-Slit Interference. Digital microscopy (вид. 3rd). Academic Press. с. 15. ISBN 0-12-374025-8. Архів оригіналу за 24 січня 2020. Процитовано 16 лютого 2019.
- ↑ Halliday, Resnick, Walker (2008). §35-4 Young's interference experiment. [[Основи фізики|Fundamentals of Physics]] (вид. Extended 8th). Wiley-India. с. 965. ISBN 81-265-1442-6. Архів оригіналу за 13 лютого 2020. Процитовано 16 лютого 2019.
{{cite book}}: Назва URL містить вбудоване вікіпосилання (довідка) - ↑ Kordt Griepenkerl (2002). §9.8.2 Diffraction by a grating. У John W Harris; Walter Benenson; Horst Stöcker; Holger Lutz (ред.). Handbook of physics. Springer. с. 307 ff. ISBN 0-387-95269-1. Архів оригіналу за 14 лютого 2020. Процитовано 16 лютого 2019.
- ↑ John C. Stover (1995). Optical scattering: measurement and analysis (вид. 2nd). SPIE Press. с. 64. ISBN 978-0-8194-1934-7. Архів оригіналу за 3 лютого 2020. Процитовано 16 лютого 2019.
- ↑ Graham Saxby (2002). Diffraction limitation. The science of imaging. CRC Press. с. 57. ISBN 0-7503-0734-X. Архів оригіналу за 11 лютого 2020. Процитовано 16 лютого 2019.
- ↑ Grant R. Fowles (1989). Introduction to Modern Optics. Courier Dover Publications. с. 117—120. ISBN 978-0-486-65957-2. Архів оригіналу за 12 лютого 2020. Процитовано 16 лютого 2019.
- ↑ James B. Pawley (1995). Handbook of biological confocal microscopy (вид. 2nd). Springer. с. 112. ISBN 978-0-306-44826-3. Архів оригіналу за 13 лютого 2020. Процитовано 16 лютого 2019.
- ↑ Ray N. Wilson (2004). Reflecting Telescope Optics I: Basic Design Theory and Its Historical Development. Springer. с. 302. ISBN 978-3-540-40106-3. Архів оригіналу за 14 лютого 2020. Процитовано 16 лютого 2019.
Джерела ред.
- Грінченко В. Т., Вовк І. В., Маципура В. Т. Основи акустики. — К.: Наукова думка, 2007. — 640 с. — ISBN 978-966-00-0622-5.
- Біленко І. І. Фізичний словник. — К. : Вища школа, 1979. — 336 с.
| Це незавершена стаття з фізики. Ви можете допомогти проєкту, виправивши або дописавши її. |







