Дельтоїд
В евклідовій геометрії дельтоїд — плоский чотирикутник, у якому дві пари суміжних сторін мають рівні довжини.
| Дельтоїд | |
|---|---|
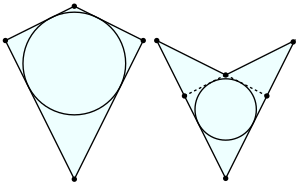 Опуклий та неопуклий дельтоїди | |
| Вид | Чотирикутник |
| Ребра і вершини | 4 |
| Група симетрії[en] | D1[en] (*), порядок 2. (Симетрія відбиття) |
| Дуальний багатокутник[en] | Рівнобічна трапеція |
| Властивості | Тангенціальний (Описується навколо кола), ортодіагональний. |
Дельтоїд є чотирикутником з симетрією відбиття відносно однієї з його діагоналей. Оскільки дельтоїд має щонайменше одну вісь симетрії, що проходить через його діагональ, то він має щонайменше два рівних протилежних кути і дві пари рівних суміжних сторін.
Дельтоїд може бути опуклим, а також неопуклим чотирикутником. Неопуклий дельтоїд також має назву дарт (дротик)[1].
Дельтоїди двох типів (опуклий і неопуклий) формують одну з плиток мозаїки Пенроуза.
Також дельтоїди є гранями кількох гранетранзитивних багатогранників, зокрема: дельтоїдального ікосотетраедра (його грані дельтоїди з трома рівними внутрішніми кутами), дельтоїдального гексеконтаедра та трапецоедрів. [2]
Окремі випадки
ред.Окремими випадками дельтоїдів є:
- прямокутний дельтоїд — опуклий дельтоїд, у якого два протилежні рівні кути прямі;
- ромб — опуклий дельтоїд, у якого всі сторони рівні, протилежні кути рівні, протилежні сторони паралельні; ромб також є окремим випадком паралелограма;
- квадрат — опуклий дельтоїд, у якого всі сторони рівні, всі кути рівні і прямі; квадрат є окремим випадком ромба.
- Серед усіх чотирикутників, чотирикутник, що має максимальне відношення периметра до діаметра (максимальна відстань між двома точками даної фігури), — це рівнодіагональний дельтоїд з кутами 60°, 75°, 150°, 75°. Його чотири вершини лежать у трьох кутах і середині однієї із сторін трикутника Рело.[3] [4]
Коли рівнодіагональний дельтоїд має довжину сторін, меншу або рівну його діагоналям (наприклад, як цей дельтоїд або квадрат), то він є одним із чотирикутників із найбільшим співвідношенням площі до діаметра.[5]
Властивості
ред.- Дельтоїд, який не є ромбом, має одну вісь симетрії.
- Кути між сторонами різної довжини рівні.
- Прямі, що містять діагоналі дельтоїда перпендикулярні, тобто дельтоїди є ортодіагональними чотирикутниками.
- Точка перетину діагоналей дельтоїда ділить одну з них навпіл. Друга діагональ (та, що є віссю симетрії) є бісектрисою протилежних кутів. У ромба обидві діагоналі точкою перетину діляться навпіл і є бісектрисами протилежних кутів.
- Одна діагональ ділить дельтоїд на два рівні трикутники. Друга діагональ ділить дельтоїд на два рівнобедрених трикутники, якщо він опуклий, і добудовує його рівнобедреним трикутником до рівнобедреного трикутника, якщо він неопуклий.
- Паралелограм Вариньона дельтоїда, вершини якого збігаються із серединами сторін дельтоїда (EFGH на мал.), є прямокутником, сторони якого паралельні діагоналям дельтоїда. Зокрема, якщо цей прямокутник є квадратом, то діагоналі дельтоїда рівні, а відрізки, що з'єднують середини протилежних сторін перпендикулярні між собою.
- Точка перетину бімедіан дельтоїда (відрізки, що сполучають середини протилежних сторін) лежить на його діагоналі.
- Чотирикутник, вершинами якого є точки дотику вписаного кола зі сторонами дельтоїда (MNQR на мал.), є рівнобедреною трапецією.
- Хорди вписаного кола, що сполучають його точки дотику зі сторонами дельтоїда, перетинаються в точці перетину діагоналей дельтоїда. Також вони мають однакову довжину.
- У будь-який опуклий дельтоїд можна вписати коло; крім цього, якщо дельтоїд не є ромбом, то існує коло, яке дотикається до продовжень всіх чотирьох сторін. Тобто будь-який опуклий дельтоїд (окрім ромба) є одночасно описаним та зовні-описаним чотирикутником. Центри вписаного та зовні-вписаного кіл лежать на прямій, що містить діагональ дельтоїда.
Для неопуклого дельтоїда можна побудувати коло, що дотикається до двох більших сторін і продовжень двох менших сторін і коло, що дотикається до двох менших сторін і продовжень двох більших сторін.
- Прямокутний дельтоїд (у якого два протилежні кути — прямі) є біцентричним чотирикутником, тобто є одночасно вписаним та описаним чотирикутником; а також і зовні-описаним чотирикутником. Центри вписаного, описаного та зовні-вписаного кіл лежать на діагоналі дельтоїда.
Формули
ред.Для дельтоїда справедливі наступні формули:
| Формули для дельтоїда | |
|---|---|
| Довжини сторін | |
| Периметр | |
| Площа | [6] |
| де r — радіус вписаного кола. | |
| Довжини діагоналей | (за теоремою косинусів) |
| , де | |
| Радіус вписаного кола | |
| Радіус зовні-вписаного кола | [7] |
| Внутрішні кути
(див. теорему косинусів) |
|
Двоїстість
ред.Дельтоїди та рівнобедрені трапеції є двоїстими один до одного чотирикутниками, що означає, що між ними існує відповідність, яка змінює елементи їх частин на протилежні, перетворюючи вершини на сторони, а сторони — на вершини.
У будь-якого дельтоїда вписане в нього коло дотикається до чотирьох його сторін у точках, що є вершинами рівнобедреної трапеції.
Для будь-якої рівнобедреної трапеції дотичні лінії до описаного кола в чотирьох вершинах утворюють чотири сторони дельтоїда. Цю відповідність також можна розглядати як приклад полярного перетворення, загального методу для відповідності точок лініям і навпаки, якщо задано фіксоване коло. Чотири вершини дельтоїда в цьому сенсі взаємні чотирьом сторонам рівнобедреної трапеції. [8]
Характеристики дельтоїдів і рівнобедрених трапецій, які відповідають одна одній за цієї двоїстості, порівнюються в таблиці нижче.[9]
| Рівнобічна трапеція | Дельтоїд |
|---|---|
| Дві пари рівних сусідніх кутів | Дві пари рівних сусідніх сторін |
| Дві рівні протилежні сторони | Два рівних протилежних кута |
| Дві протилежні сторони мають спільний перпендикуляр, що проходить через їх середини | Два протилежні кути мають спільну бісектрису |
| Вісь симетрії проходить через протилежні сторони | Вісь симетрії проходить через протилежні кути |
| Має описане коло | Має вписане коло |
Паркети з дельтоїдами
ред.Опуклий дельтоїд з кутами 72°, 72°, 72°, 144° та неопуклий дельтоїд з кутами 36°, 72°, 36°, 216° формують одну з плиток мозаїки Пенроуза, аперіодичної плоскої мозаїки, відкритої фізиком-математиком Роджером Пенроузом. [10]
Коли дельтоїд має кути, які при його вершинах на одній стороні сумарно дорівнюють для деякого натурального числа 𝑛 , тоді масштабованими копіями цього дельтоїда можна замостити площину фрактальною розеткою, у якій центральна точка послідовно оточується все більшими кільцями з 𝑛 дельтоїдів. [11] Ці розетки можна використовувати для вивчення явища непружного колапсу, коли система рухомих частинок, що стикаються при непружних зіткненнях, об’єднується в одній точці.[12]
Дельтоїд з кутами 60°, 90°, 120°, 90° також може утворити паркет, яким можна замостити площину; при відзеркаленні дельтоїда відносно його ребер утворюється дельтоїдальна тригексагональна плитка, що замощує площину правильними шестикутниками та рівносторонніми трикутниками. [7]
Примітки
ред.- ↑ Charter, Kevin; Rogers, Thomas (1993), The dynamics of quadrilateral folding, Experimental Mathematics, 2 (3): 209—222, doi:10.1080/10586458.1993.10504278, MR 1273409
- ↑ Grünbaum, B. (1960), On polyhedra in having all faces congruent, Bulletin of the Research Council of Israel, 8F: 215–218 (1960), MR 0125489
- ↑ Ball, D. G. (1973), A generalisation of , The Mathematical Gazette, 57 (402): 298—303, doi:10.2307/3616052, JSTOR 3616052, S2CID 125396664
- ↑ Griffiths, David; Culpin, David (1975), Pi-optimal polygons, The Mathematical Gazette, 59 (409): 165—175, doi:10.2307/3617699, JSTOR 3617699, S2CID 126325288
- ↑ Audet, Charles; Hansen, Pierre; Svrtan, Dragutin (2021), Using symbolic calculations to determine largest small polygons, Journal of Global Optimization, 81 (1): 261—268, doi:10.1007/s10898-020-00908-w, MR 4299185, S2CID 203042405
- ↑ Beamer, James E. (May 1975), The tale of a kite, The Arithmetic Teacher, 22 (5): 382—386, doi:10.5951/at.22.5.0382, JSTOR 41188788
- ↑ а б Alsina, Claudi; Nelsen, Roger B. (2020), Section 3.4: Kites, A Cornucopia of Quadrilaterals, The Dolciani Mathematical Expositions, т. 55, Providence, Rhode Island: MAA Press and American Mathematical Society, с. 73—78, ISBN 978-1-4704-5312-1, MR 4286138; see also antiparallelograms, p. 212
- ↑ Robertson, S. A. (1977), Classifying triangles and quadrilaterals, The Mathematical Gazette, 61 (415): 38—49, doi:10.2307/3617441, JSTOR 3617441, S2CID 125355481
- ↑ De Villiers, Michael (2009), Some Adventures in Euclidean Geometry, Dynamic Mathematics Learning, с. 16, 55, ISBN 978-0-557-10295-2
- ↑ Gardner, Martin (January 1977), Extraordinary nonperiodic tiling that enriches the theory of tiles, Mathematical Games, Scientific American, т. 236, № 1, с. 110—121, Bibcode:1977SciAm.236a.110G, doi:10.1038/scientificamerican0177-110, JSTOR 24953856
- ↑ Fathauer, Robert (2018), Art and recreational math based on kite-tiling rosettes, у Torrence, Eve; Torrence, Bruce; Séquin, Carlo; Fenyvesi, Kristóf (ред.), Proceedings of Bridges 2018: Mathematics, Art, Music, Architecture, Education, Culture, Phoenix, Arizona: Tessellations Publishing, с. 15—22, ISBN 978-1-938664-27-4
- ↑ Chazelle, Bernard; Karntikoon, Kritkorn; Zheng, Yufei (2022), A geometric approach to inelastic collapse, Journal of Computational Geometry, 13 (1): 197—203, doi:10.20382/jocg.v13i1a7, MR 4414332
- ↑ Smith, David; Myers, Joseph Samuel; Kaplan, Craig S.; Goodman-Strauss, Chaim (19 березня 2023). An aperiodic monotile. arXiv:2303.10798 [cs, math]. Процитовано 27 березня 2023.
Література
ред.- Josefsson, Martin (2011), When is a tangential quadrilateral a kite? (PDF), Forum Geometricorum, 11: 165—174
- Josefsson, Martin (2012), Maximal area of a bicentric quadrilateral (PDF), Forum Geometricorum, 12: 237—241, MR 2990945
- Jepsen, Charles H.; Sedberry, Trevor; Hoyer, Rolf (2009), Equidissections of kite-shaped quadrilaterals (PDF), Involve: A Journal of Mathematics, 2 (1): 89—93, doi:10.2140/involve.2009.2.89, MR 2501347
- Suay, Juan Miguel; Teira, David (2014), Kites: the rise and fall of a scientific object (PDF), Nuncius (journal), 29 (2): 439—463, doi:10.1163/18253911-02902004
Посилання
ред.- Дельтоїд // Універсальний словник-енциклопедія. — 4-те вид. — К. : Тека, 2006.
- Weisstein, Eric W. Kite(англ.) на сайті Wolfram MathWorld.
- Kite(англ.) на сайті Polytope Wiki.
- Kite (англ.)
- Area of a Kite (англ.) Формули площі та інтерактивна анімація.