Розподіл Кантора

Розподіл Кантора — розподіл ймовірностей, функція розподілу ймовірностей якого є функцією Кантора.

Кантора
Функція розподілу ймовірностей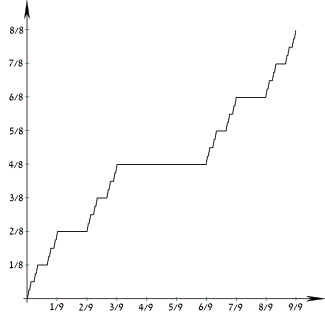
Параметри	немає
Носій функції	Множина Кантора
Розподіл імовірностей	немає
Функція розподілу ймовірностей (cdf)	Функція Кантора
Середнє	1/2
Медіана	будь-де у [1/3, 2/3]
Мода	n/a
Дисперсія	1/8
Коефіцієнт асиметрії	0
Коефіцієнт ексцесу	−8/5
Твірна функція моментів (mgf)	$e^{t/2}\prod _{k=1}^{\infty }\cosh \left({\frac {t}{3^{k}}}\right)$
Характеристична функція	$e^{it/2}\prod _{k=1}^{\infty }\cos \left({\frac {t}{3^{k}}}\right)$

Цей розподіл не має ані функції густини ймовірності, ані функції ймовірностей, оскільки, хоча його функція розподілу є неперервною функцією, розподіл не є абсолютно неперервним щодо міри Лебега, а також не має точкових мас. Таким чином, він є ані дискретним, ані абсолютно неперервним розподілом ймовірностей, ані їхнім поєднанням. Він є швидше прикладом сингулярного розподілу.

Характеристика

Носієм розподілу Кантора є множина Кантора, власне перетин (нескінченного числа) множин:

${\begin{aligned}C_{0}={}&[0,1]\\[8pt]C_{1}={}&[0,1/3]\cup [2/3,1]\\[8pt]C_{2}={}&[0,1/9]\cup [2/9,1/3]\cup [2/3,7/9]\cup [8/9,1]\\[8pt]C_{3}={}&[0,1/27]\cup [2/27,1/9]\cup [2/9,7/27]\cup [8/27,1/3]\cup \\[4pt]{}&[2/3,19/27]\cup [20/27,7/9]\cup [8/9,25/27]\cup [26/27,1]\\[8pt]C_{4}={}&[0,1/81]\cup [2/81,1/27]\cup [2/27,7/81]\cup [8/81,1/9]\cup [2/9,19/81]\cup [20/81,7/27]\cup \\[4pt]&[8/27,25/81]\cup [26/81,1/3]\cup [2/3,55/81]\cup [56/81,19/27]\cup [20/27,61/81]\cup \\[4pt]&[62/81,21/27]\cup [8/9,73/81]\cup [74/81,25/27]\cup [26/27,79/81]\cup [80/81,1]\\[8pt]C_{5}={}&\cdots \end{aligned}}$

Розподіл Кантора — унікальний розподіл ймовірностей, для якого для будь-якого C_t (t ∈ { 0, 1, 2, 3, … }), ймовірність того, що певний інтервал у C_t, що містить розподілену Кантором випадкову величину, дорівнює 2^-t на кожному з 2^t інтервалів.

Моменти

За симетрією легко переконатися, що для випадкової величини X, що має такий розподіл, її очікуване значення E(X) = 1/2, і що всі непарні центральні моменти X є 0.

Закон повної дисперсії може бути використаний для знаходження дисперсії var(X) наступним чином. Для вищевказаного набору C₁ нехай Y=0, якщо X ∈ [0,1/3], і 1, якщо X ∈ [2/3,1]. Тоді:

${\begin{aligned}\operatorname {var} (X)&=\operatorname {E} (\operatorname {var} (X\mid Y))+\operatorname {var} (\operatorname {E} (X\mid Y))\\&={\frac {1}{9}}\operatorname {var} (X)+\operatorname {var} \left\{{\begin{matrix}1/6&{\mbox{з імовірністю}}\ 1/2\\5/6&{\mbox{з імовірністю}}\ 1/2\end{matrix}}\right\}\\&={\frac {1}{9}}\operatorname {var} (X)+{\frac {1}{9}}\end{aligned}}$

З цього ми отримуємо:

$\operatorname {var} (X)={\frac {1}{8}}.$

Вираз замкнутої форми для будь-якого парного центрального моменту можна знайти, попередньо отримавши парні кумулятори

$\kappa _{2n}={\frac {2^{2n-1}(2^{2n}-1)B_{2n}}{n\,(3^{2n}-1)}},\,\!$

де В_2n є 2n-им числом Бернуллі, а потім виразити моменти як функції кумулянтів.

Джерела

• Hewitt, E.; Stromberg, K. (1965). Real and Abstract Analysis. Berlin-Heidelberg-New York: Springer-Verlag. (англ.)
• Hu, Tian-You; Lau, Ka Sing (2002). Fourier Asymptotics of Cantor Type Measures at Infinity. Proc. A.M.S. Т. 130, № 9. с. 2711—2717. (англ.)
• Knill, O. (2006). Probability Theory & Stochastic Processes. India: Overseas Press.
• Mattilla, P. (1995). Geometry of Sets in Euclidean Spaces. San Francisco: Cambridge University Press. (англ.)