Граф Коксетера
Граф Коксетера — 3-регулярний граф з 28 вершинами і 42 ребрах[1]. Усі кубічні дистанційно-регулярні графи відомі[2], граф Коксетера — один з 13-ти таких графів.
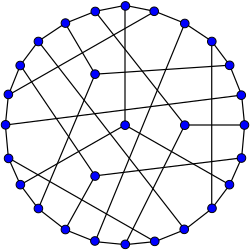 Граф Коксетера | |
| Вершин | 28 |
|---|---|
| Ребер | 42 |
| Радіус | 4 |
| Діаметр | 4 |
| Обхват | 7 |
| Автоморфізм | 336 (ПЛГ2(7)) |
| Хроматичне число | 3 |
| Хроматичний індекс | 3 |
| Число черг | 2 |
| Властивості | симетричний кубічний дистанційно-регулярний дистанційно-транзитивний гіпогамільтонів[en] |
Властивості
ред.Хроматичне число графа 3, хроматичний індекс дорівнює 3, радіус дорівнює 4, діаметр — 4 обхват — 7. Граф є також вершинно 3-зв'язним і реберно 3-зв'язним.
Граф Коксетера є гіпогамільтонівським графом — сам по собі він не містить гамільтонових циклів, але видалення будь-якої вершини робить його гамільтоновим. Число прямолінійних схрещень графа Коксетера дорівнює 11 і це мінімальний відомий кубічний граф з таким числом схрещень, хоча графи з 26 вершинами і числом схрещень 11 існувати можуть[3].
Граф Коксетера можна побудувати з меншого дистанційно-регулярного графа Хівуда шляхом створення вершини для кожного 6-циклу в графі Хивуда і ребра для кожної незв'язної пари 6-циклів.[4]
Граф Коксетера також можна отримати з графа Гофмана — Синглтона. Візьмемо будь яку вершину v графа Гофмана — Синглтона. Існує незалежна множина розміру 15, яка містить v. Видалимо 6 сусідів v і цю незалежну множину, включаючи v залишимо.
Алгебраїчні властивості
ред.Група автоморфізмів графа Коксетера — це група порядку 336[5]. Вона діє транзитивно на вершини і ребра графа, тому граф Коксетера є симетричним. Граф має автоморфизми, які переводять будь-яку вершину в будь-яку іншу і будь-яке ребро будь-яке інше ребро. У «списку Фостера» граф Коксетера, зазначений як F28A, є єдиним кубічним симетричним графом з 28 вершинами[6].
Граф Коксетера однозначно визначається за його спектром, тобто множиною власних значень матриці суміжності графа[7].
Як скінченно зв'язний вершинно-транзитивний граф, що не містить гамільтонових циклів, граф Коксетера є контрприкладом варіанту гіпотези Ловаса, але канонічна формулювання гіпотези вимагає наявності гамільтонового циклу.
Відомо лише п'ять вершинно-транзитивних графів без гамільтонових циклів — повний граф «K»2, граф Петерсена, граф Коксетера і два графи, отримані з графів Петерсена і Коксетера шляхом заміни кожної вершини трикутником[8].
Характеристичний поліном графа Коксетера дорівнює . Граф є єдиним графом з таким поліномом, що і дозволяє однозначно визначити граф Коксетера за його спектром.
Галерея
ред.-
Граф, отриманий видаленням будь-якого ребра з графа Коксетера є гамільтоново-зв'язним.
-
Хроматичне число графа Коксетера дорівнює 3.
-
Число прямолінійних схрещень графа Коксетера дорівнює 11.
Примітки
ред.- ↑ Weisstein, Eric W. Coxeter Graph(англ.) на сайті Wolfram MathWorld.
- ↑ A. E. Брауер, A. M. Cohen, A. Neumaier. Distance-Regular Graphs. — New York : Springer-Verlag, 1989. (англ.)
- ↑ послідовність A110507 з Онлайн енциклопедії послідовностей цілих чисел, OEIS
- ↑ Italo J. Dejter. From the Coxeter graph to the graph Klein // Journal of теорія Графів. — 2011. — arXiv:1002.1960. — DOI:..
- ↑ Royle, G. F028A data[недоступне посилання з квітня 2019]
- ↑ M. Conder, P. Dobcsányi, «Trivalent Symmetric Graphs Up to 768 Vertices.» J. Combin. Math. Combin. Comput. 40, 41-63, 2002.
- ↑ E. R. van Dam and W. H. Haemers, Spectral Characterizations of Some Distance-Regular Graphs. J. Алгебраїчна Combin. 15, pages 189—202, 2003
- ↑ Royle, G. «Cubic Symmetric Graphs (Foster The Census).» [Архівовано 20 липня 2008 у Wayback Machine.]