Індуковане розшарування
Індуковане розшарування — розшарування , індуковане відображенням і розшаруванням , де — підпростір прямого добутку , що складається з пар , виду:
- ,
для яких , а проєкція за означенням задана як .
Шаром f*E над точкою b′ простору B′ є шар у E над f(b′). Тобто як множина f*E є диз'юнктним об'єднанням всіх цих шарів.
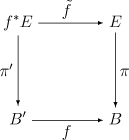
Відображення індукованого розшарування в вихідне розшарування, задане формулою є морфізмом розшарувань, що накриває . При цьому комутативна діаграма утворює декартовий квадрат:
Властивості
ред.- Для кожної точки обмеження на шар є гомеоморфізмом.
- Для будь-якого розшарування і морфізму розшарувань , що накриває , існує один і тільки один -морфізм , що задовольняє співвідношенню .
- Розшарування, індуковані ізоморфними розшаруваннями, є ізоморфними. Розшарування, індуковане постійним відображенням є ізоморфним тривіальному розшаруванню.
- Для будь-якого перетину розшарування відображення , задане формулою , є перетином індукованого розшарування і задовольняє співвідношенню .
- Якщо (U, φ) є локальною тривіалізацією розшарування E, тоді (f−1U, ψ) є локальною тривіалізацією f*E де
- Тобто у цьому випадку f*E теж є локально тривіальним розшаруванням над B′ з шаром F.
- Якщо локально тривіальне розшарування E → B також має структурну групу G з функціями перетворення tij (для локальних тривіалізацій {(Ui, φi)}, тоді G також буде структурною групою індукованого розшарування f*E. Функції перетворення розшарування f*E рівні
- Якщо E → B є векторним чи головним розшаруванням, то таким же розшаруванням є f*E. У випадку головних розшарувань права дія групи G на f*E визначається як
- Звідси випливає, що є еквіваріантним відображенням і тому задає морфізм головних розшарувань.
Література
ред.- Steenrod, N. (1951). The Topology of Fibre Bundles. Princeton: Princeton University Press. ISBN 0-691-00548-6.
- Husemoller, D. (1994). Fibre Bundles. Graduate Texts in Mathematics. Т. 20 (вид. Third). New York: Springer-Verlag. ISBN 978-0-387-94087-8.