| Ортогональні поліноми
|
|
|
| Лежандра
|
| Відкриті
|
Адрієн-Марі Лежандр
|
| Формула
|
![{\displaystyle P_{n}(x)={1 \over 2^{n}n!}{d^{n} \over dx^{n}}\left[(x^{2}-1)^{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad969113cbd9ce7c159d27350ece1e855f91c2a2)
|
| Диференціальне рівняння
|
![{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P_{n}(x)\right]+n(n+1)P_{n}(x)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/460225fdcc5f208e5e3f0010e17978139cc1e26f)
|
| Визначені на
|
![{\displaystyle \ [-1,+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cebaa4dd56eed99a7ac7bfd533ca9685682d90e)
|
| Вага
|
1
|
| Норма
|

|
| Примітки
|
|
Поліноми Лежандра — ортогональні поліноми на інтервалі ![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01) .
.
Поліноми Лежандра можна отримати з системи поліномів  за допомогою ортогоналізації Грама-Шмідта.
за допомогою ортогоналізації Грама-Шмідта.
Можуть бути обчислені за допомогою прямих формул:
![{\displaystyle P_{n}(x)={1 \over 2^{n}n!}{d^{n} \over dx^{n}}\left[(x^{2}-1)^{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad969113cbd9ce7c159d27350ece1e855f91c2a2)
або за рекурентними:

Вони є розв'язками диференційного рівняння Лежандра:
![{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P_{n}(x)\right]+n(n+1)P_{n}(x)=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd51c7228067db4bea119843fb19c6caab834954)
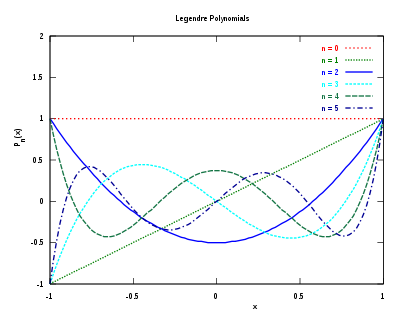 Графіки поліномів Лежандра порядку
Графіки поліномів Лежандра порядку 
Генератриса для многочленів Лежандра дорівнює

Перші 9 поліномів Лежандра:










Умова ортогональності справджується на інтервалі :
-
де — дельта-символ Кронекера.
Приєднані функції Лежандра
ред.
Приєднані функції Лежандра визначаються за формулою:
-
яку можна також представити у вигляді:
-
При функція збігається з .
Їх часто називають приєднаними поліномами Лежандра, хоча насправді ці функції не поліноми.
Приєднані функції Лежандра є розв'язками диференціального рівняння:
-
або еквівалентного йому:
-

![{\displaystyle P_{n}(x)={1 \over 2^{n}n!}{d^{n} \over dx^{n}}\left[(x^{2}-1)^{n}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ad969113cbd9ce7c159d27350ece1e855f91c2a2)
![{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P_{n}(x)\right]+n(n+1)P_{n}(x)=0}](https://wikimedia.org/api/rest_v1/media/math/render/svg/460225fdcc5f208e5e3f0010e17978139cc1e26f)
![{\displaystyle \ [-1,+1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3cebaa4dd56eed99a7ac7bfd533ca9685682d90e)

![{\displaystyle [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51e3b7f14a6f70e614728c583409a0b9a8b9de01)


![{\displaystyle {d \over dx}\left[(1-x^{2}){d \over dx}P_{n}(x)\right]+n(n+1)P_{n}(x)=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd51c7228067db4bea119843fb19c6caab834954)











