Відцентрова сила
Відцентро́ва си́ла (англ. centrifugal force) в механіці — багатозначне визначення, що склалося як історично, так і через невпорядкованість науково-технічної термінології, і розбіжності в науково-технічному середовищі. Відцентрові сили стосуються криволінійного руху тіла або матеріальної точки і, згідно з Великою радянською енциклопедією (ВРЕ) та низкою інших енциклопедичних джерел, тлумачаться так:

Відцентрова сила ─сила, з якою матеріальна точка, котра рухається, діє на тіло (зв'язок), що утруднює свободу руху точки і змушує її рухатися криволінійно. Чисельно відцентрова сила дорівнює , де ─ маса точки, ─ її швидкість, ─ радіус кривини траєкторії, і спрямована по головній нормалі до траєкторії від центру кривини (від центру кола під час руху точки по колу). Відцентрова сила і доцентрова сила чисельно дорівнюють одна одній і спрямовані уздовж однієї прямої в протилежні боки, але прикладені до різних тіл ─ як сили дії і протидії.
Наприклад, у разі обертання в горизонтальній площині прив'язаного до мотузки тягарця, доцентрова сила діє з боку мотузки на тягарець, змушуючи його рухатися по колу, а відцентрова сила діє з боку тягарця на мотузку, натягує її і, при досить великій швидкості руху, може обірвати.
Коли до рішення задач динаміки, застосовують принцип Д'Аламбера, терміну відцентрова сила надають іноді інший сенс і називають відцентровою силою складову сили інерції матеріальної точки, спрямовану по головній нормалі до траєкторії.
Зрідка відцентровою силою називають також нормальну складову переносної сили інерції при складанні рівнянь відносного руху.
По суті в цьому визначенні під словосполученням відцентрова сила маються на увазі три різних значення цього терміна. Розгляньмо їх докладніше.
1) Відцентрова сила в першому значенні — ньютонова відцентрова сила.
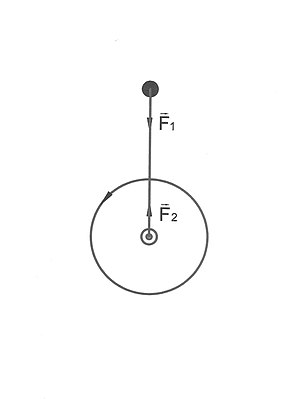
На малюнку зображено: диск, що рівномірно обертається навколо вертикальної осі, мотузку, один кінець якої з'єднано з центром диска, а до іншого кінця прив'язано кульку. (Система відліку інерціальна, пов'язана з поверхнею Землі).
На кульку діє сила натягу мотузки , спрямована до центру обертання, яка викривляє траєкторію руху кульки і змушує її рухатися по колу. Ця сила називається доцентровою. Відцентрова сила також створюється натягом мотузки, але вона прикладена до іншого тіла — диска. Отже, відцентрова і доцентрова сили прикладені до різних тіл. (Мотузка мається на увазі нерозтяжною). Доцентрова і відцентрова сили у даному контексті виступають як звичайні сили дії і протидії за третім законом Ньютона. Своєю назвою вони зобов'язані винятково напряму, по якому вони діють (до центру або від центру) і ніякого іншого смислового навантаження не несуть. Деякі автори, слідуючи академіку Ішлінському, називають ці сили ньютоновими або справжніми силами.
2) відцентрова сила в другому її значенні називається д'аламберова відцентрова сила.
Д'аламберова відцентрова сила є окремим випадком д'аламберової сили інерції, яка штучно вводиться в розрахункову схему сил для отримання формальної можливості запису рівнянь динаміки у вигляді простіших рівнянь статики. Вона не існує насправді, не може бути ані відчута, ані виміряна, й належить до категорії фіктивних, несправжніх або псевдосил.
3) У третьому значенні відцентровою силою називається «Нормальна складова переносної сили інерції при складанні рівнянь відносного руху».[1] Ця сила є окремим випадком інерційних сил, що виникають в неінерціальних системах відліку.
Пояснімо це на прикладі.
Уявімо собі диск, що рівномірно обертається навколо вертикальної осі з кутовою швидкістю . На диску в радіальному напрямі встановлено напрямну, на яку надіто кульку й пружину розтягування. Один кінець пружини сполучено з кулькою, а інший — зачеплено за вісь диска. Відносно диска, що обертається, кулька перебуває в стані спокою. При рівномірному обертанні диска тангенціальні сили і тангенціальні прискорення відсутні, а сила розтягування пружини , що діє на кульку у радіальному напрямі дорівнює добутку маси кульки на нормальне (доцентрове) прискорення .
або
,
де — радіус-вектор, проведений з центру кульки до центру диска.

Але таку картину побачить спостерігач, що перебуває в інерційній системі відліку, , пов'язаній з поверхнею Землі. Якщо зв'язати неінерціальну систему відліку з рівномірно обертальним диском, то, з точки зору спостерігача, що знаходиться в цій системі, диск разом з тілом спочиває, а рівновага кульки пояснюється дією двох сил: сили, яка прагне віддалити її від центру диска — відцентрової сили інерції і сили розтягування пружини , спрямованої до центру:
або
За термінологією, запропонованою академіком О. Ю. Ішлінським, відцентрові сили інерції, іноді називають ейлеровими силами. (Як відомо, Л. Ейлер вперше використовував рухливі системи координат для розв'язування складних завдань механіки).[3] Прикладами цих відцентрових сил інерції є сили, що діють на пасажирів транспорту на крутих поворотах, на льотчиків, що здійснюють віражі й фігури вищого пілотажу, й на учасників різних циркових і паркових атракціонів (американські гірки, центрифуга, каруселі тощо).
На відміну від фіктивних д'аламберових сил, ейлерови відцентрові сили інерції мають ознаки, які зближують їх з реальними силами. Ці сили можливо відчути й виміряти. Питання про визнання ейлерових сил справжніми силами досі залишається дискусійним.
Історична довідка
ред.Поняття сили інерції й відцентрової сили вперше згадуються у Ньютона в його класичній книзі «Математичні начала натуральної філософії». Говорячи про «вроджену силу матерії», тобто про властивість будь-якого тіла зберігати свій стан спокою або рівномірного прямолінійного руху за відсутності дії будь-яких сил, Ньютон не дає чіткого визначення сили інерції й змішує поняття інерція — стан, в якому перебуває тіло, з поняттям інертність — властивість тіла. Ньютон також використовує термін відцентрова сила, але розглядає її як реальну фізичну силу, тобто в першому значенні, згідно з Великою радянською енциклопедією. Подібне змішання термінів зберігається і досі.[4]
Мабуть, жодне з положень теоретичної механіки не викликало стільки суперечок і плутанини, як принцип Д'аламбера. У 20-ті роки минулого століття проти нього виступили філософи, які звинувачували автора в недіалектичності, оскільки вивчення руху по Д'аламберу зводиться до вивчення статичної задачі — рівноваги, яка є окремим випадком задачі динамічної.[5]
У 1936—1937 роках в радянській пресі виникла дискусія про сили інерції, зокрема, про відцентрову силу, між інженерами — практиками і механіками — теоретиками з питання критики поглядів на інерцію відомого радянського науковця — механіка Л. Б. Левенсона, який писав про те, що практики давно вже ведуть розрахунки машин, враховуючи реальність сил інерції, а теоретики, не рахуючись з фактами, наполягають на нереальності сил інерції й стверджують, що ці сили зовсім не існують. 1940 року вийшла книга професора С. Е. Хайкіна «Що таке сили інерції», в якій він виступав з позицій науковців — прихильників реальності інерційних сил.[6]
Відомі кілька запеклих дискусій в середовищі фахівців з механіки з приводу того, чи слід вважати сили інерції реальними силами, або ж відносити їх до уявних чи фіктивних. Остання така дискусія пройшла в Інституті проблем механіки АН СРСР між прихильниками академіка О. Ю. Ішлінського (вважав, що сили інерції фіктивні) та прихильниками академіка Л. І. Сєдова (вважав, що сили інерції справжні) на Всесоюзній нараді «Основи класичної механіки та їх роль у викладанні механіки» (Москва, 1-8 жовтня 1985 р). Видатні науковці посварилися й розійшлися, не розв'язавши остаточно питання.
Різні думки про відцентрові сили в навчальній і науковій літературі
ред.Численні дискусії з приводу відцентрових сил мають, по суті, термінологічний зміст, оскільки все залежить від способу визначення поняття сила, і того, що саме розуміють під терміном відцентрова сила. Розгляньмо думки й доводи обох сторін.
Прихильники Ішлінського «справжньою» відцентровою силою називають силу протидії, яка в інерційній системі відліку, згідно з третім законом механіки, прикладена до зв'язку. Д'Аламберови і ейлерови відцентрові сили вважають несправжніми, вигаданими, тому що д'аламберови сили не підкоряються другому і третьому законам Ньютона, а ейлерови інерційні відцентрові сили не підкоряються третьому закону Ньютона.
Наприклад, в курсі фізики Фріш і Тіморевої т. I § 21 стверджується: «доцентрова і відцентрова сили — це ті дві сили, існування яких обумовлено третім законом Ньютона; прикладені вони до різних тіл. Наприклад, в разі обертання каменю, прив'язаного до мотузки, доцентрова сила прикладена до каменя, а відцентрова — до мотузки…»[7] До цього слід додати, що мова йде про інерційні системи відліку. Подібне визначення доцентрової та відцентрової сил дається й у шкільному курсі фізики Пьоришкіна.[8] У наступному параграфі (§ 22) курсу фізики Фріш і Тіморевої йдеться про інерційну відцентрову силу, що діє в обертальній системі, яку, на думку авторів, «іноді називають інерціальною відцентровою силою. Її не слід змішувати з тією дійсною відцентровою силою, про яку йшла мова в § 21.»[9].
Проти назв доцентрова і відцентрова для ньютонових сил взаємодії, при обертальному руху в інерціальній системі відліку, у противників Ішлінського є ряд заперечень.
На думку Хайкіна ці назви, строго кажучи, не потрібні. Цілком достатньо знати, що сила, прикладена до обертального тіла з боку мотузки, є діюча, а сила, прикладена з боку тіла до мотузки — протидіюча. Назви сил доцентрова і відцентрова ніякого смислового навантаження, крім вказівки напряму їх дії, не несуть, зате створюють помилкове враження про існування якихось нових особливих сил, котрі відносяться винятково до обертального руху, що є шкідливою помилкою: відцентрові й доцентрові сили в інерціальній системі відліку це звичайні сили взаємодії.[10]
До речі, в багатьох підручниках і навчальних посібниках силу, яка створює доцентрове прискорення в інерціальній системі називають доцентровою, але протидійну їй силу, що діє на зв'язок, називають силою реакції, або, взагалі, ніяк не називають за непотрібністю.[11][12][13]
Однак, головною точкою протистояння прихильників Ішлінського і прихильників Сєдова є питання справжності або фіктивності ейлерових відцентрових сил інерції. Якщо з питання фіктивності д'аламберових сил немає особливих розбіжностей, то питання про реальність ейлерових сил інерції перебуває в центрі дискусії. Використання ейлерових сил інерції, зокрема, відцентрової сили інерції, дозволяє застосовувати другий закон Ньютона в неінерційних системах відліку. Але, на відміну від д'аламберових сил, що вводяться штучно, ейлерови відцентрові сили інерції виникають при переході з інерціальної системи відліку в неінерціальну й зникають при зворотному переході. Ці сили мають ознаки, які зближують їх зі справжніми силами, оскільки їх можливо відчути й виміряти, а в певних випадках неможливо відрізнити від справжніх сил. Єдиним серйозним аргументом не вважати відцентрові сили інерції справжніми силами є той факт, що джерело їх походження невідоме через відсутність взаємодійного тіла. Тому вони не підкоряються третьому закону Ньютона — рівності сил дії і протидії. На думку Д. В. Сивухина: рух тіл під дією сил інерції аналогічний руху у зовнішніх силових полях.
Сили інерції завжди є зовнішніми по відношенню до будь-якої системи матеріальних тіл. Щодо реальності або фіктивності сил інерції, то відповідь на це питання залежить від змісту, який вкладається в слова реальний і фіктивний. Якщо дотримуватися ньютонівської механіки, згідно з якою всі сили повинні бути наслідком взаємодії тіл, то на сили інерції слід дивитися як на оманливі сили, що зникають в інерційних системах відліку. Однак, така точка зору необов'язкова. Всі взаємодії здійснюються за допомогою силових полів і передаються з кінцевими швидкостями. І на сили інерції можна дивитися як на дії, яким піддаються тіла з боку якихось реальних силових полів.[14]
Схожу думку висловив Г. В. Єгоров:
Численні дискусії з приводу реальності сил інерції мають, по суті, термінологічний характер, тому що все залежить від способу визначення поняття сила. Якщо, як це зазвичай робиться, визначати силу як фізичну величину, яка є мірою кількісної дії інших тіл або полів на дане тіло, то сила інерції є уявної силою, тому що ми не можемо вказати її джерело ─ тіло, з боку якого вона діє. Однак, якщо силу тлумачити як причину прискорення тіла, то сила інерції нічим не гірше інших сил. Незастосування третього закону Ньютона в цьому випадку принципового значення не має, оскільки для будь-якої фізичної системи сили інерції завжди будуть зовнішніми силами, а третій закон Ньютона істотний лише для внутрішніх сил, що діють між тілами, які входять в систему. Для будь-якого з тіл, що перебуває в неінерціальній системі відліку, сили інерції є зовнішніми; отже, тут немає замкнутих систем.— Г. В. Єгоров, [4]
Безлад і плутанина, пов'язані з визначенням відцентрової сили
ред.Відсутність єдиної загальновизнаної термінології в підручниках та науковій літературі з фізики й механіки, що стосується відцентрових сил інерції, призводить до плутанини понять, помилок, парадоксів, а інколи й до повного нерозуміння суті питання. Один із прикладів такого роду, описано в Загальному курсі фізики Д. В. Сивухіна. Автор пише:
Відцентрові сили, як і всякі сили інерції, існують лише в системах відліку, що рухаються прискорено і зникають при переході до інерціальних систем. Забувши це, можна прийти до парадоксів, які часто ставлять в тупик школярів. Ось один з найпоширеніших парадоксів такого типу.Нехай тіло рухається по колу. На нього діють дві сили: доцентрова , спрямована до центру кола, і відцентрова , спрямована в протилежний бік. Ці сили рівні за модулем і врівноважують одна одну.
За законом інерції тіло повинно рухатися прямолінійно і рівномірно.
Суперечність виникла тому, що рух стали відносити до нерухомої (інерційної) системі відліку. А в цій системі ніяких відцентрових сил не існує. Є тільки одна доцентрова сила , яка і надає тілу прискорення.
Плутанина відбувається через те, що в технічній механіці термін відцентрова сила іноді вживають в зовсім іншому сенсі. Відцентровою силою називають силу реакції з якою тіло A, що обертається по колу, діє на тіло B, що примушує його здійснювати це обертання. Рівну і протилежно спрямовану силу, з якою тіло B діє на тіло A, називають доцентровою … Доцентрова і відцентрова сили, у такому розумінні, завжди прикладені до різних тіл…— Д. В. Сивухіна
Однак, розуміючи відцентрову силу в цьому сенсі, яку в підручнику Фріш і Тіморевої названо дійсною відцентровою силою, і вважати, що вона віддаляє тіло яке обертається, від центру, цілком безглуздо, оскільки цю силу до тіла, що обертається, не прикладено.[15]
Єдине, в чому можна «дорікнути» Сивухіну, це те, що вказаний ним парадокс ніби відноситься лише до невдалих школярів. Таке ж «розуміння» відцентрових і доцентрових сил нерідко зустрічається в студентів, аспірантів, інженерів і навіть у викладачів фізики.
Ось приклад з дуже поширеної в США книги Л. Елліот і У. Уілкокса «Физика», яка вийшла в перекладі російською мовою під ред. А. І. Китайгородского 1975 року.
У розділі 17 цієї книги розглядається найпростіший випадок рівномірного руху по колу кульки, прив'язаної до мотузки. До кульки прикладені чотири сили: — рушійна сила, спрямована по дотичній до окружності і, рівна їй за величиною, але протилежно спрямована сила інерції а також сила , що спрямована до центру кола, і рівна їй за величиною сила , яка спрямована у протилежному напрямку (від центру).
Далі по тексту:
Сила , тягне тіло до центру і звертає тіло з прямолінійного шляху, називається доцентровою силою. Але доцентрова сила ─ це не єдина сила, що діє під час руху по колу, тому що, відповідно до третього закону Ньютона, сили завжди діють парами. Якщо існує доцентрова сила, то повинна бути і інша сила , рівна їй за величиною, але протилежна за напрямком. Ця сила називається відцентровою силою…»— Л. Елліот, У. Уілкокс, [16]
Здавалося б, судячи з написаного, йдеться про інерціальну систему й відцентрову силу в її першому значенні, згідно ВРЕ. Але, в наступному абзаці читаємо:
Дію відцентрової сили відчувають на собі пасажири, що їдуть в автобусі або автомобілі, коли машина робить крутий поворот.— Л. Елліот, У. Уілкокс, [16]
Отже йдеться про неінерціальну систему відліку і вже про відцентрову силу інерції в другому її значенні, а це якраз той самий, описаний Сивухіним випадок безладу й плутанини, але вже не в голові школяра, а в навчальній літературі.
З усього сказаного можна зробити висновок: доки не буде розроблено єдиної системи термінології, слід уважно ставитися до виразу «відцентрова сила», й у кожному певному випадку з'ясовувати, якого поняття він стосується.
Див. також
ред.Примітки
ред.- ↑ а б БСЭ та 1969—1978.
- ↑ Савельев, И.В., 1989, с. 122─123.
- ↑ Ишлинский, А.Ю., 1987, с. 18.
- ↑ а б Егоров, Г.В., 2013.
- ↑ Гулиа, Н.В., 1982, с. 27.
- ↑ Гулиа, Н.В., 1982, с. 48—50.
- ↑ Фриш, Тиморева., 1962, с. 65.
- ↑ Пёрышкин, А. В., 1957, с. 22.
- ↑ Фриш, Тиморева., 1962, с. 70.
- ↑ Хайкин С.Э., 1967, с. 110—111.
- ↑ Милковская Л. Б., 1972, с. 138.
- ↑ Ландсберг Г.С., 1985, с. 231.
- ↑ Селезнёв Ю. А., 1969, с. 76—77.
- ↑ Сивухин Д.В., 2005, с. 359.
- ↑ Сивухин Д.В., 2005, с. 365─366.
- ↑ а б Эллиот, Уилкокс., 1975, с. 192─193.
Джерела
ред.- Большая советская энциклопедия : в 30 т. / главн. ред. А. М. Прохоров. — 3-е изд. — М. : «Советская энциклопедия», 1969—1978. (рос.)
- Гулиа Н.В. Инерция. — М. : «Наука», 1982. — 152 с.
- Егоров Г.В. Силы инерции. — Вестник Брянского государственного университета, 2013. — № 1.
- Ишлинский А.Ю. Классическая механика и силы инерции. — М. : «Наука», 1987. — 320 с.
- Ландсберг Г.С. Элементарный учебник физики. — М. : «Наука», 1985. — Т. 1. — 606 с.
- Милковская Л. Б. Повторим физику. — М. : «Высшая школа», 1972. — 608 с.
- Пёрышкин А.В. Курс физики (часть вторая). — 9е. — М. : «Учпедгиз», 1957. — 216 с.
- Савельев И.В. Курс физики. — М. : «Наука», 1989. — Т. 1. — 496 с. — ISBN 5-02-014052-x:5-02-014430-4.
- Селезнёв Ю. А. Основы элементарной физики. — 3е. — М. : «Наука», 1969. — 496 с.
- Сивухин Д.В. Общий курс физики. — 4е. — М. : Физматлит; МФТИ, 2005. — Т. 1. — 560 с. — ISBN 5-9221-0225-7;5-89155-078-4.
- Фриш, Тиморева. Курс общей физики. — 10е. — М. : Физматлит, 1962. — Т. 1. — 468 с.
- Хайкин С.Э. Силы инерции и невесомость. — М. : «Наука», 1967. — 312 с.
- Эллиот, Уилкокс. Физика. — 3е. — М. : «Наука», 1975. — 736 с.
















