Поверхня Шерка

У математиці поверхня Шерка (названа на честь Генріха Шерка) є прикладом мінімальної поверхні. Шерк описав дві повні вкладені мінімальні поверхні в 1834 році; його перша поверхня є подвійно періодичною поверхнею, друга — одноперіодичною. Вони були третім нетривіальним прикладом мінімальних поверхонь (першими двома були катеноїд і гелікоїд). Дві поверхні є спряженими одна з одною.

Анімація перетворення першої та другої поверхні Шерка однієї в одну: вони є членами одного асоційованого сімейства мінімальних поверхонь.

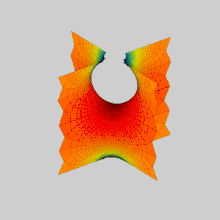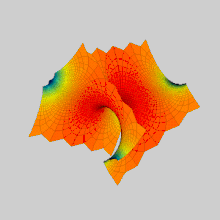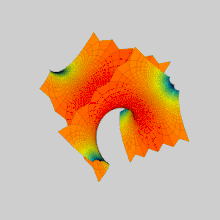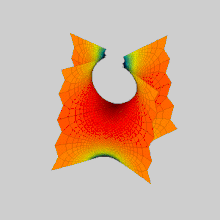
Поверхні Шерка виникають при вивченні деяких граничних задач мінімальних поверхонь і при вивченні гармонійних дифеоморфізмів гіперболічного простору.

Перша поверхня Шерка

Перша поверхня Шерка є асимптотичною для обидвох взаємноортогональних нескінченних сімейств паралельних площин, які зустрічаються в околі z=0 у шаховому порядку перемикаючих арок. Вона містить нескінченну кількість прямих вертикальних ліній.

Побудова простої поверхні Шерка

Елементарна комірка STL першої поверхні Scherk

П'ять елементарних комірок, розміщених разом

Розглянемо таку задачу мінімальної поверхні на квадраті в евклідовій площині: для натурального числа n знайдимо мінімальну поверхню Σ _n задану графіком певної функції

$u_{n}:\left(-{\frac {\pi }{2}},+{\frac {\pi }{2}}\right)\times \left(-{\frac {\pi }{2}},+{\frac {\pi }{2}}\right)\to \mathbb {R}$

такий, що

$\lim _{y\to \pm \pi /2}u_{n}\left(x,y\right)=+n{\text{ for }}-{\frac {\pi }{2}}<x<+{\frac {\pi }{2}},$

$\lim _{x\to \pm \pi /2}u_{n}\left(x,y\right)=-n{\text{ for }}-{\frac {\pi }{2}}<y<+{\frac {\pi }{2}}.$

Тобто u _n задовольняє рівняння мінімальної поверхні

$\mathrm {div} \left({\frac {\nabla u_{n}(x,y)}{\sqrt {1+|\nabla u_{n}(x,y)|^{2}}}}\right)\equiv 0$

і

$\Sigma _{n}=\left\{(x,y,u_{n}(x,y))\in \mathbb {R} ^{3}\left|-{\frac {\pi }{2}}<x,y<+{\frac {\pi }{2}}\right.\right\}.$

Чим, якщо існує, є гранична поверхня, якщо n прямує до нескінченності? Відповідь дав Г. Шерк у 1834 р.: гранична поверхня Σ є графіком

$u:\left(-{\frac {\pi }{2}},+{\frac {\pi }{2}}\right)\times \left(-{\frac {\pi }{2}},+{\frac {\pi }{2}}\right)\to \mathbb {R} ,$

$u(x,y)=\log \left({\frac {\cos(x)}{\cos(y)}}\right).$

Тобто поверхня Шерка на квадраті є

$\Sigma =\left\{\left.\left(x,y,\log \left({\frac {\cos(x)}{\cos(y)}}\right)\right)\in \mathbb {R} ^{3}\right|-{\frac {\pi }{2}}<x,y<+{\frac {\pi }{2}}\right\}.$

Більш загальні поверхні Шерка

Подібні задачі мінімальної поверхні можна розглядати й на інших чотирикутниках евклідової площини. Цю ж задачу можна також розглянути про чотирикутники в гіперболічній площині. У 2006 році Гарольд Розенберг і Паскаль Коллін використовували гіперболічні поверхні Шерка для побудови гармонійного диффеоморфізму з комплексної площини на гіперболічну площину (одиничний диск з гіперболічною метрикою), тим самим спростувавши гіпотезу Шоена–Яу .

Друга поверхня Шерка

Друга поверхня Шерка

STL елементарна комірка другої поверхні Шерка

Друга поверхня Шерка глобально виглядає як дві ортогональні площини, перетин яких складається з послідовності тунелів у позмінних напрямках. Її перетини з горизонтальними площинами урворють гіперболи.

Задається неявним рівнянням:

$\sin(z)-\sinh(x)\sinh(y)=0$

Вона має параметризацію Вейєрштрасса-Еннепера $f(z)={\frac {4}{1-z^{4}}}$, $g(z)=iz$ і її можна параметризувати:

$x(r,\theta )=2\Re (\ln(1+re^{i\theta })-\ln(1-re^{i\theta }))=\ln \left({\frac {1+r^{2}+2r\cos \theta }{1+r^{2}-2r\cos \theta }}\right)$

$y(r,\theta )=\Re (4i\tan ^{-1}(re^{i\theta }))=\ln \left({\frac {1+r^{2}-2r\sin \theta }{1+r^{2}+2r\sin \theta }}\right)$

$z(r,\theta )=\Re (2i(-\ln(1-r^{2}e^{2i\theta })+\ln(1+r^{2}e^{2i\theta }))=2\tan ^{-1}\left({\frac {2r^{2}\sin 2\theta }{r^{4}-1}}\right)$

для $\theta \in [0,2\pi )$ і $r\in (0,1)$ . Це дає один період поверхні, який потім можна симетрично розширити по осі z.

Поверхня була узагальнена Г. Карчером до сідловидної вежі - сімейства періодичних мінімальних поверхонь.

Цю поверхню в літературі іноді називають п’ятою поверхнею Шерка. Аби знизити можливості для плутанини, можна називати її одноперіодичною поверхнею Шерка або вежею Шерка.

Ланки

• Sabitov, I.Kh. (2001), Scherk surface, у Hazewinkel, Michiel (ред.), Математична енциклопедія, Springer, ISBN 978-1-55608-010-4
• Scherk's first surface in MSRI Geometry [1]
• Scherk's second surface in MSRI Geometry [2]
• Scherk's minimal surfaces in Mathworld [3]