Метод Нелдера — Міда

Метод Нелдера — Міда (метод симплексного спуску, метод амеби, або політопний метод)) є популярним чисельним методом, що використовується для пошуку мінімуму або максимуму цільової функції в багатовимірному просторі. Це метод прямого пошуку (на основі порівняння функцій) і часто застосовується до нелінійних задач оптимізації, для яких похідні можуть не бути відомі. Проте, підхід Нелдера-Міда є евристичним методом пошуку, який може сходитися до нестаціонарних точок, стикаючись з проблемами, які можуть бути розв'язані альтернативними методами.

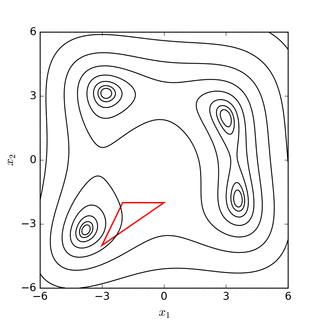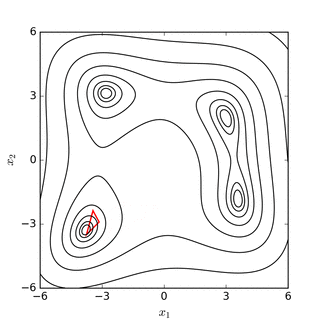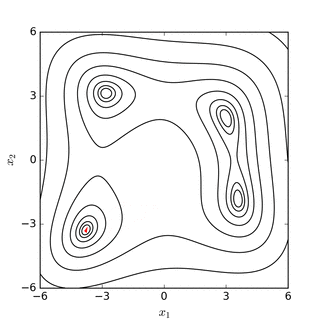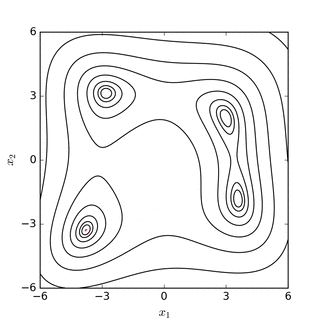
Послідовні симплекси в функції Нелдера-Міда для Функції Розенброка (вгорі) та функції Химмельблау (внизу)

Мінімальний пошук Нелдера-Міда функції Сімінеску. Упорядкування симплексних вершин за їх значенням, причому 1 має найменше (найкраще) значення.

Метод Нелдера — Міда запропонували Джон Нелдер і Роджер Мід у 1965 році, як варіант модифікації методу Спендлі.

Загальний опис

У методі використовується поняття симплекса, який є спеціальним політопом n + 1 вершин в n вимірах. Приклади симплексів включають відрізок на лінії, трикутник на площині, тетраедр у тривимірному просторі тощо.

Метод апроксимує локальний оптимум задачі з n змінними, коли цільова функція змінюється плавно і є унімодальною. Типові реалізації мінімізують функції, максимум $f(\mathbf {x} )$ можна знайти за допомогою мінімізації $-f(\mathbf {x} )$.

Наприклад, інженер підвісного моста повинен вибрати, якою має бути товщина кожної стійки, кабелю і причалу. Ці елементи взаємозалежні, але нелегко візуалізувати вплив зміни стану будь-якого конкретного елемента. Моделювання таких складних конструкцій часто є надзвичайно обчислювально складним для запуску, можливо, тому що вони потребують більше годин на виконання. Метод Нелдера — Міда вимагає у вихідному варіанті не більше двох оцінок на ітерацію, за винятком описаної пізніше операції стягування, що є перевагою порівняно з іншими методами оптимізації прямого пошуку. Однак загальна кількість ітерацій пропонованого оптимуму може бути великою.

Метод у n вимірах зберігає набір n+1 тестових точок, розташованих як симплекс. Потім він екстраполює поведінку цільової функції, виміряної в кожній тестовій точці, щоб знайти нову тестову точку і замінити одну зі старих тестових точок на нову, це складає основний цикл методу. Найпростіший підхід полягає в тому, щоб замінити найгіршу точку точкою, відбитою через центроїд решти n точок. Якщо ця точка краща, ніж краща поточна точка, то ми можемо спробувати розтягнути експоненціально по цій лінії. З іншого боку, якщо ця нова точка не є набагато кращою, ніж попередня величина, то ми переходимо до наступного значення, тому ми стягуємо симплекс у кращу точку. Інтуїтивне пояснення алгоритму представлено в:

Метод спадання симплекса тепер виконує ряд кроків, більшість кроків просто переміщує точку симплекса, де функція набуває найбільшого значення («найвища точка») через протилежну сторону симплекса до нижньої точки. Ці кроки називаються відбиттями, і вони побудовані для збереження обсягу симплекса (і, отже, збереження його невиродженості). Коли це може зробити, метод розширює симплекс в тому чи іншому напрямку, щоб зробити великі кроки. Коли він досягає «найнижчої точки», метод починає рухатися в поперечному напрямку і намагається просунутися вздовж лінії спадання. У ситуації, коли симплекс намагається «пройти крізь голку», то він стискається у всіх напрямках, стягуючи себе навколо своєї найнижчої (кращої) точки.

На відміну від сучасних методів оптимізації, евристика Нелдера — Міда може сходитися до нестаціонарної точки, якщо задача не задовольняє сильнішим умовам, ніж це необхідно для сучасних методів. Сучасні поліпшення евристики Нелдера-Мід відомі з 1979 року.

Існує багато варіацій залежно від фактичної природи розв'язуваної проблеми. Звичайний варіант використовує невеликий симплекс постійного розміру, який приблизно відповідає напрямку градієнта (який дає найшвидший спуск). Візуалізуйте маленький трикутник на карті висоти, що перевертається по долині до найнижчої точки на місцевості. Цей метод також відомий «як гнучкий метод багатогранника». Це, однак, має тенденцію до поганого виконання методу, описаного в цій статті(?), оскільки він робить невеликі, непотрібні кроки в областях, що представляють малий інтерес.

Один з можливих варіантів алгоритму Нелдера-Міда

(Це близько до процедури, яка описана в оригінальній статті Нелдера-Міда.)

Метод Нелдера — Міда, застосований до функції Розенброка

Ми намагаємося мінімізувати функцію $f(\mathbf {x} )$, де $\mathbf {x} \in \mathbb {R} ^{n}$. Наші поточні контрольні точки є $\mathbf {x} _{1},\ldots ,\mathbf {x} _{n+1}$.

1. Порядок відповідно до значень у вершинах:

$f(\mathbf {x} _{1})\leq f(\mathbf {x} _{2})\leq \cdots \leq f(\mathbf {x} _{n+1}).$

Перевірте, чи слід зупинити метод. Дивіться Завершення нижче. Іноді неправильно називають «збіжністю».

2. Розрахуйте $\mathbf {x} _{o}$, центроїд всіх точок, окрім $\mathbf {x} _{n+1}$.

3. Відбиття

Обчислити симетрично віддзеркалену або, як будемо казати далі, відбиту точку $\mathbf {x} _{r}=\mathbf {x} _{o}+\alpha (\mathbf {x} _{o}-\mathbf {x} _{n+1})$ з $\alpha >0$.

Якщо відбита краща, ніж друга найгірша, але не краща, ніж краща, тобто $f(\mathbf {x} _{1})\leq f(\mathbf {x} _{r})<f(\mathbf {x} _{n})$,

тоді отримайте новий симплекс, замінивши найгіршу точку $\mathbf {x} _{n+1}$ симетрично віддзеркаленою точкою $\mathbf {x} _{r}$, і перейдіть до кроку 1.

4.Розширення

Якщо відбита точка є найкращою точкою досі, $f(\mathbf {x} _{r})<f(\mathbf {x} _{1})$,

потім обчислити розширену точку $\mathbf {x} _{e}=\mathbf {x} _{o}+\gamma (\mathbf {x} _{r}-\mathbf {x} _{o})$ з $\gamma >1$.

Якщо розширена точка краще відбитої точки, $f(\mathbf {x} _{e})<f(\mathbf {x} _{r})$,

отримуємо новий симплекс, замінюючи найгіршу точку $\mathbf {x} _{n+1}$ розширеною точкою $\mathbf {x} _{e}$, і перейдіть до кроку 1;

інакше отримуємо новий симплекс, замінюючи найгіршу точку $\mathbf {x} _{n+1}$ відбитою точкою $\mathbf {x} _{r}$ і перейдіть до кроку 1.

5. Скорочення

Тут напевно $f(\mathbf {x} _{r})\geq f(\mathbf {x} _{n})$. (Зауважте що $\mathbf {x} _{n}$ це друге чи «наступне» після найвищого.): Обчислити контрактну точку до $\mathbf {x} _{c}=\mathbf {x} _{o}+\rho (\mathbf {x} _{n+1}-\mathbf {x} _{o})$ з $0<\rho \leq 0.5$.

Якщо контрактна точка краща, ніж найгірша точка, тобто $f(\mathbf {x} _{c})<f(\mathbf {x} _{n+1})$,

потім отримують новий симплекс шляхом заміни найгіршої точки $\mathbf {x} _{n+1}$ на контрактну точку $\mathbf {x} _{c}$ і переходять до кроку 1;

6. Стягування

Замініть всі точки, крім кращих ($\mathbf {x} _{1}$) з

$\mathbf {x} _{i}=\mathbf {x} _{1}+\sigma (\mathbf {x} _{i}-\mathbf {x} _{1})$,і перейдіть до кроку 1.

Примітка: $\alpha$, $\gamma$, $\rho$ і $\sigma$ відповідно коефіцієнти відбиття, розширення, скорочення і стягування. Стандартними значеннями $\alpha =1$, $\gamma =2$, $\rho =1/2$ та $\sigma =1/2$.

Для відбиття, оскільки $\mathbf {x} _{n+1}$ це вершина з вищою асоційованою величиною серед вершин, можливо буде менше значення при відбитті $\mathbf {x} _{n+1}$ у бік протилежній стороні, утвореній всіма вершинами $\mathbf {x} _{i}$, крім $\mathbf {x} _{n+1}$.

Для розширення, якщо точка відбиття $\mathbf {x} _{r}$ i є новим мінімумом уздовж вершин, можна розраховувати знайти шукані значення вздовж напрямку від $\mathbf {x} _{o}$ до $\mathbf {x} _{r}$.

Що стосується скорочення, якщо $f(\mathbf {x} _{r})>f(\mathbf {x} _{n})$, то можна очікувати, що краще значення буде всередині симплекса, утвореного всіма вершинами $\mathbf {x} _{i}$.

Нарешті, стягування обробляє рідкісний випадок, коли скорочення від найбільшої точки збільшує $f$, що не може трапитись досить близько до несингулярного мінімуму. У цьому випадку ми скорочуємо у бік найнижчої точки в очікуванні знайти простішу ландшафт. Проте, Неш зазначає, що арифметика зі скінченною точністю іноді не може фактично стягнути симплекс, і виконати перевірку того, що розмір насправді зменшився.

Початковий симплекс

Початковий симплекс важливий. Дійсно, занадто малий початковий симплекс може призвести до локальних пошуків, отже, метод може легше зупинитися. Отже, цей симплекс повинен залежати від природи проблеми. А проте, оригінальна стаття запропонувала симплекс, де дається початкова точка $\mathbf {x} _{1}$, а інші генеруються з фіксованим кроком по кожному виміру по черзі. Таким чином, метод чутливий до масштабування змінних, які складають $\mathbf {x}$.

Завершення

Критерії необхідні для розриву ітераційного циклу. Нелдер і Мід використовували зразкове стандартне відхилення значень функцій поточного симплекса. Якщо вони опускаються нижче певних обмежень, то цикл зупиняється і найнижча точка в симплексі видається як запропонований оптимум. Зауважимо, що дуже «плоска» функція може мати майже однакові значення функцій над великим доменом, так що рішення буде чутливим до обмежень. Неш додає тест на усадку як ще один критерій переривання роботи. Зауважте, що програми припиняються, тоді як ітерації можуть сходитися.

Див. також

• Метод прямого пошуку
• COBYLA
• NEWUOA
• LINCOA
• Нелінійний сполучений градієнтний метод
• Алгоритм Левенберга — Марквардта
• Бройден–Флетчер–Голдфарб-Шано або BFGS метод
• Диференціальна еволюція
• Метод Гука — Дживса
• CMA-ES

Література

• Avriel, Mordecai (2003). Nonlinear Programming: Analysis and Methods. Dover Publishing. ISBN 978-0-486-43227-4.
• Coope, I. D.; Price, C. J. (2002). Positive Bases in Numerical Optimization. Computational Optimization & Applications. 21 (2): 169—176. doi:10.1023/A:1013760716801.
• Gill, Philip E.; Murray, Walter; Wright, Margaret H. (1981). Methods for Multivariate Non-Smooth Functions. Practical Optimization. New York: Academic Press. с. 93–96. ISBN 978-0-12-283950-4.
• Kowalik, J.; Osborne, M. R. (1968). Methods for Unconstrained Optimization Problems. New York: Elsevier. с. 24–27. ISBN 0-444-00041-0.
• Swann, W. H. (1972). Direct Search Methods. У Murray, W. (ред.). Numerical Methods for Unconstrained Optimization. New York: Academic Press. с. 13—28. ISBN 978-0-12-512250-4.

Посилання

• Nelder–Mead (Simplex) Method
• Nelder–Mead (Downhill Simplex) explanation and visualization with the Rosenbrock banana function
• John Burkardt: Nelder–Mead code in Matlab — note that a variation of the Nelder–Mead method is also implemented by the Matlab function fminsearch.
• nelder-mead — A Python implementation of the Nelder–Mead method
• SOVA 1.0 (freeware) — Simplex Optimization for Various Applications
• [1] — HillStormer, a practical tool for nonlinear, multivariate and linear constrained Simplex Optimization by Nelder Mead.