Добуток Адамара

У математиці добуток Адамара (також відомий як добуток Шура або покомпонентний добуток) — це бінарна операція над двома матрицями однакової розмірності, у результаті котрої створюється нова матриця де кожен елемент ij це добуток елементів ij початкових матриць. Операція названа на честь, або французького математика Жака Адамара, або німецького математика Ісая Шура.

Добуток Адамара оперує з двома матрицями однакової розмірності і створює нову матрицю ідентичної розмірності.

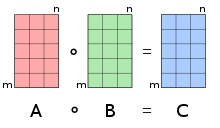
Добуток Адамара це асоціативна та дистрибутивна операція, і на відміну від добутку матриць також комутативна операція.

Визначення

Для двох матриць $A,B$ котрі мають однакову розмірність $m\times n$ добуток адамара позначається як $A\circ B$ і визначений як покомпонентний добуток двох матриць:

$(A\circ B)_{i,j}=(A)_{i,j}\cdot (B)_{i,j}$

Для двох матриць, котрі мають різні розмірності, добуток Адамара не визначений.

Приклад

Приклад використання добутку Адамара для двох матриць A та B розмірністю 2x3

$\left({\begin{array}{ccc}\mathrm {a} _{11}&\mathrm {a} _{12}&\mathrm {a} _{13}\\\mathrm {a} _{21}&\mathrm {a} _{22}&\mathrm {a} _{23}\\\end{array}}\right)\circ \left({\begin{array}{ccc}\mathrm {b} _{11}&\mathrm {b} _{12}&\mathrm {b} _{13}\\\mathrm {b} _{21}&\mathrm {b} _{22}&\mathrm {b} _{23}\\\end{array}}\right)=\left({\begin{array}{ccc}\mathrm {a} _{11}\,*\mathrm {b} _{11}\ &\mathrm {a} _{12}\,*\mathrm {b} _{12}&\mathrm {a} _{13}\,*\mathrm {b} _{13}\\\mathrm {a} _{21}\,*\mathrm {b} _{21}&\mathrm {a} _{22}\,*\mathrm {b} _{22}&\mathrm {a} _{23}\,*\mathrm {b} _{23}\\\end{array}}\right)$

Властивості

Добуток Адамара це комутативна, асоціативна та дистрибутивна операція,

$A\circ B=B\circ A,$

$A\circ (B\circ C)=(A\circ B)\circ C,$

$A\circ (B+C)=A\circ B+A\circ C.$

Змішані добутки

$(A\otimes B)\circ (C\otimes D)=(A\circ C)\otimes (B\circ D)$, де $\otimes$ — добуток Кронекера

$(A\bullet B)\circ (C\bullet D)=(A\circ C)\bullet (B\circ D)$, де $\bullet$ — торцевий добуток.

$(A\bullet B)(C\ast D)=(AC)\circ (BD)$, де $\ast$ — стовпцевий добуток Хатрі-Рао.

Використання

Добуток Адамара використовується у алгоритмах стиснення з втратами, наприклад, JPEG.

У програмних пакетах MATLAB та GNU Octave, дана операція використовується як стандартна операція множення масивів та позначається символом * .
Операція добутку над векторними типами даних у GPGPU технологіях програмування також реалізована за принципом добутку Адамара. Інші примітивні математичні операції над векторними типами даних реалізовані як покомпонентні операції над їх компонентами.

Блокова версія

Проникаючий торцевий добуток

Проникаючий торцевий добуток

Цей тип матричної операції спирається на добуток Адамара і дозволяє поелементно перемножити $p\times g$ матрицю $\mathbf {A}$ на довільну кількість блоків тієї ж розмірності $p\times g$, що утворюють блокову матрицю $\mathbf {B}$:

$\mathbf {A} [\circ ]\mathbf {B} =\left[{\begin{array}{c | c | c | c }\mathbf {A} \circ \mathbf {B} _{1}&\mathbf {A} \circ \mathbf {B} _{2}&\ ...\ &\mathbf {A} \circ \mathbf {B} _{n}\end{array}}\right]$.

Наприклад, для

$\mathbf {A} =\left[{\begin{array}{c}1&2&3\\4&5&6\\7&8&9\end{array}}\right],\quad \mathbf {B} =\left[{\begin{array}{c | c | c }\mathbf {B} _{1}&\mathbf {B} _{2}&\mathbf {B} _{3}\end{array}}\right]=\left[{\begin{array}{c c c | c c c | c c c }1&4&7&2&8&14&3&12&21\\8&20&5&10&25&40&12&30&6\\2&8&3&2&4&2&7&3&9\end{array}}\right]$

отримаємо:

$\mathbf {A} [\circ ]\mathbf {B} =\left[{\begin{array}{c c c | c c c | c c c }1&8&21&2&16&42&3&24&63\\32&100&30&40&125&240&48&150&36\\14&64&27&14&32&18&49&24&81\end{array}}\right]$.

Основні властивості:

$\mathbf {A} [\circ ]\mathbf {B} =\mathbf {B} [\circ ]\mathbf {A}$;

$\mathbf {M} \bullet \mathbf {M} =\mathbf {M} [\circ ](\mathbf {M} \otimes \mathbf {1} ^{\textsf {T}})$,

де $\bullet$ — символ торцевого добутку матриць.

$\mathbf {c} \bullet \mathbf {M} =\mathbf {c} [\circ ]\mathbf {M}$, де $\mathbf {c}$ — вектор.

Даний вид матричного добутку був запропонований в 1998 р. Слюсарем В. І. для опису відгуків цифрової антенної решітки з неідентичними приймальними каналами. Крім того, цей добуток дозволяє формалізувати процес функціонування згорткової нейромережі. Наприклад, якщо розглянути вказану матрицю $\mathbf {A}$ як масив пікселів зображення на вході нейромережного алгоритму, то блоки матриці $\mathbf {B}$ будуть відповідати різним наборам коефіцієнтів для формування згорткового шару в кількох паралельных каналах обробки зображення нейромережею.

Операція проникаючого торцевого добутку вектора і матриці реалізована в бібліотеці машинного навчання TensorFlow за допомогою оператора «tf.multiply».

Див. також

• Добуток Кронекера
• Добуток Хатрі-Рао

Джерела

• Гантмахер Ф. Р. Теория матриц. — 5-е. — М: : Физматлит, 2010. — 559 с. — ISBN 5-9221-0524-8.(рос.)
• Ланкастер П. Теория матриц. — 2. — Москва : Наука, 1982. — 272 с.(рос.)
• Р.Хорн, Ч.Джонсон. Матричный анализ. — М: : Мир, 1989. — 653 с.(рос.)