Граф Грея
В математичній галузі теорії графів, неорієнтований граф Грея є двочастковим графом з 54 вершинами і 81 ребром. Це кубічний граф, де кожна вершина має рівно три ребра. Цей граф відкритий Меріаном К. Греєм в 1932 році (результат не був оприлюднений), потім виявлений незалежно Баувером (Bouwer) у 1968 року у відповідь на питання, яке задав Джон Фолкман[en] у 1967 році. Граф Грея є першим відомим прикладом кубічного графу, що має алгебраїчну властивість бути реберним, але не вершинно-транзитивним (див. нижче).
| Граф Грея | |
|---|---|
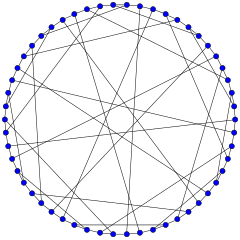 The Gray graph | |
| Названо на честь | Marion Cameron Gray |
| Вершин | 54 |
| Ребер | 81 |
| Радіус | 6 |
| Діаметр | 6 |
| Обхват | 8 |
| Автоморфізм | 1296 |
| Хроматичне число | 2 |
| Хроматичний індекс | 3 |
| Число черг | 2 |
| Властивості | Кубічний Напівсиметричний Гамільтонів граф Двочастковий граф |
Граф Грея має хроматичне число що дорівнює 2, хроматичний індекс 3, радіус 6 і діаметр 6. Він також є 3-вершинно-зв'язний та 3-реберно-зв'язний не планарний граф.
Побудова
ред.Граф Грея може бути побудований (Bouwer, 1972) з 27 точок, сітки 3×3×3 і 27 паралельних прямих через ці точки. Ця колекція з точок і прямих утворює проективні конфігурації: через кожну точку проходять три прямі, і на кожній прямій лежать три точки. В цій конфігурації граф Грея є графом Леві; він має вершину для кожної точки у кожному рядку конфігурації, і ребра для кожної пари точки з прямою, якщо точка лежить на прямій. Ця конструкція узагальнюється для будь-якої розмірності N ≥ 3, поступаючись N-валентному графу Леві, алгебраїчними властивостями, близькими до властивостей графу Грея. Граф Грея з'являється у вигляді різного роду графів Леві. Він є першим в нескінченному сімействі аналогічно побудованих кубічних графів.
Марушич і Пісанскі (Marušič та Pisanski, 2000) дають декілька альтернативних методів побудови графу Грея. Як і у будь-якого двочасткового графу, у нього немає непарних циклів довжини, а також відсутні цикли з чотирьох або шести вершин, тому обхват графу Грея дорівнює 8. Найпростіша орієнтована поверхня, на якій граф Грея може впроваджуватися має рід 7 (Marušič, Pisanski та Wilson, 2005).
Граф Грея та Гамільтонів граф можуть бути побудовані з LCF-нотації:
![{\displaystyle [-25,7,-7,13,-13,25]^{9}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f8ef56d09a853e7609c7a0a263afb19fe4cacde9)
Алгебраїчні властивості
ред.Група автоморфізмів графу Грея — це група 1296 порядку. Вона діє транзитивно на ребрах графу, але не на своїх вершинах, отже, вона є симетричною, тому приймає кожне ребро будь-якому іншому ребру, але не приймає кожну вершину будь-якій іншій вершині. Вершини, які відповідають точкам базової конфігурації можуть бути тільки симетричні іншим вершинам, які відповідають точкам, і вершини, відповідні прямі, можуть бути симетричні тільки до інших вершин, які відповідають прямим. Тому граф Грея — це напівсиметричний граф і мінімальний можливий кубічний напівсиметричний граф.
Характеристичний поліном графу Грея:
Галерея
ред.-
граф Грея -
Хроматичне число графу Грея дорівнює 2. -
Хроматичний індекс графу Грея дорівнює 3. -
Базова конфігурація графу Грея.
Посилання
ред.- Bouwer, I. Z. (1972), On edge but not vertex transitive regular graphs, Journal of Combinatorial Theory, Series B, 12: 32—40, doi:10.1016/0095-8956(72)90030-5.
- Folkman, J. (1967), Regular line-symmetric graphs, Journal of Combinatorial Theory, 3 (3): 533—535, doi:10.1016/S0021-9800(67)80069-3.
- Marušič, Dragan; Pisanski, Tomaž (2000), The Gray graph revisited, Journal of Graph Theory, 35: 1—7, doi:10.1002/1097-0118(200009)35:1<1::AID-JGT1>3.0.CO;2-7.
- Marušič, Dragan; Pisanski, Tomaž; Wilson, Steve (2005), The genus of the Gray graph is 7, European Journal of Combinatorics, 26 (3–4): 377—385, doi:10.1016/j.ejc.2004.01.015.
- Monson, B.; Pisanski, T.; Schulte, E.; Ivic-Weiss, A. (2007), Semisymmetric Graphs from Polytopes, Journal of Combinatorial Theory, Series A, 114 (3): 421—435, doi:10.1016/j.jcta.2006.06.007