Центровані багатокутні числа
Центровані багатокутні числа — це клас плоских -кутних фігурних чисел (), одержуваних такою геометричною побудовою. Спочатку на площині фіксується певна центральна точка. Потім навколо неї будується правильний -кутник з точками вершин, кожна сторона містить дві точки (див. малюнок). Далі зовні будуються нові шари -кутників, причому кожна їхня сторона на новому шарі містить на одну точку більше, ніж у попередньому шарі, тобто, починаючи з другого шару, кожен наступний шар містить на більше точок, ніж попередній. Загальне число точок усередині кожного шару і приймається за центроване багатокутне число (точка в центрі вважається початковим шаром)[1].
Приклади побудови центрованих багатокутних чисел:
| Трикутні | Квадратні | П'ятикутні | Шестикутні |
|---|---|---|---|
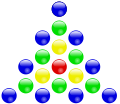
|
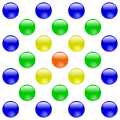
|
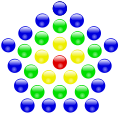
|

|
З побудови видно, що центровані багатокутні числа виходять як часткові суми такого ряду: (наприклад, центровані квадратні числа, для яких утворюють послідовність: ) Цей ряд можна записати як , звідки видно, що в дужках — породжувальний ряд класичних трикутних чисел. Отже, кожну послідовність центрованих -кутних чисел, починаючи з 2-го елементу, можна подати як де — послідовність трикутних чисел. Наприклад, центровані квадратні числа — це помножені на 4 трикутні числа плюс 1, породжувальний ряд для них має вигляд: [2]
Загальна формула для -го центрованого -кутного числа :
-
({{{3}}})
Зведена таблиця
ред.| Число кутів k | Тип числа | Початок послідовності | Посилання на OEIS |
|---|---|---|---|
| 3 | Центровані трикутні числа | 1, 4, 10, 19, 31, … | A005448 |
| 4 | Центровані квадратні числа | 1, 5, 13, 25, 41, … | A001844 |
| 5 | Центровані п'ятикутні числа | 1, 6, 16, 31, 51, … | A005891 |
| 6 | Центровані шестикутні числа | 1, 7, 19, 37, 61, … | A003215 |
| 7 | Центровані семикутні числа | 1, 8, 22, 43, 71, … | A069099 |
| 8 | Центровані восьмикутні числа | 1, 9, 25, 49, 81, … | A016754 |
| 9 | Центровані дев'ятикутні числа | 1, 10, 28, 55, 91, … | A060544 |
| 10 | Центровані десятикутні числа | 1, 11, 31, 61, 101, … | A062786 |
і так далі.
Примітки
ред.- ↑ Деза Е., Деза М., 2016, с. 39—40.
- ↑ Деза Е., Деза М., 2016, с. 40—41.
Література
ред.- Виленкин Н. Я., Шибасов Л. П. Шибасова 3. Ф. За страницами учебника математики: Арифметика. Алгебра. Геометрия. — М. : Просвещение, 1996. — С. 30. — ISBN 5-09-006575-6.
- Глейзер Г. И. [1] — М. : Просвещение, 1964. — 376 с. Архівовано з джерела 4 грудня 2017
- Деза Е., Деза М. Фигурные числа. — М. : МЦНМО, 2016. — 349 с. — ISBN 978-5-4439-2400-7.
Посилання
ред.- Weisstein, Eric W. Центроване багатокутне число(англ.) на сайті Wolfram MathWorld.
- Фігурні числа [Архівовано 23 листопада 2018 у Wayback Machine.] (рос.)











