Бета-функція

У математиці бета-функцією ($\mathrm {B}$-функцією, бета-функцією Ейлера чи інтегралом Ейлера I роду) називається наступна спеціальна функція від двох змінних:

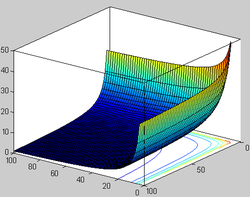Графік бета-функції при дійсних аргументах

$\mathrm {\mathrm {B} } (x,y)=\int \limits _{0}^{1}t^{x-1}(1-t)^{y-1}\,dt$,

визначена при $\Re (x)>0$, $\Re (y)>0$.

Бета-функція була досліджена Ейлером і Лежандром, а назву їй дав Жак Біне.

Властивості

Бета-функція симетрична відносно перестановки змінних, тобто

$\mathrm {\mathrm {B} } (x,y)=\mathrm {\mathrm {B} } (y,x)$.

Бета-функцію можна виразити через інші функції:

$\mathrm {\mathrm {B} } (x,\;y)={\frac {\Gamma (x)\Gamma (y)}{\Gamma (x+y)}}$,

де $\Gamma (x)$ — Гамма-функція;

$\mathrm {\mathrm {B} } (x,\;y)=2\int \limits _{0}^{\pi /2}\sin ^{2x-1}\theta \cos ^{2y-1}\theta \,d\theta ,\qquad \Re (x)>0,\ \Re (y)>0$;

$\mathrm {\mathrm {B} } (x,\;y)=\int \limits _{0}^{\infty }{\frac {t^{x-1}}{(1+t)^{x+y}}}\,dt,\qquad \Re (x)>0,\ \Re (y)>0$;

$\mathrm {\mathrm {B} } (x,\;y)={\frac {1}{y}}\sum _{n=0}^{\infty }(-1)^{n}{\frac {(y)_{n+1}}{n!(x+n)}}$,

де $(x)_{n}$ — нижній факторіал, рівний $x\cdot (x-1)\cdot (x-2)\cdot \ldots \cdot (x-n+1)$.

Подібно тому як гама-функція для цілих чисел є узагальненням факторіала, бета-функція є узагальненням біноміальних коефіцієнтів зі зміненими параметрами:

$\mathrm {C} _{n}^{k}={\frac {1}{(n+1)\mathrm {B} (n-k+1,\;k+1)}}$.

Похідні

Частинні похідні у бета-функції наступні:

${\partial \over \partial x}\mathrm {B} (x,\;y)=\mathrm {B} (x,\;y)\left({\Gamma ^{\prime }(x) \over \Gamma (x)}-{\Gamma ^{\prime }(x+y) \over \Gamma (x+y)}\right)=\mathrm {B} (x,\;y)(\psi (x)-\psi (x+y))$.

Неповна бета-функція

Неповна бета-функція — це узагальненням бета-функції,що заміняє визначений інтеграл невизначеним:

$\mathrm {B} _{x}(a,\;b)=\int \limits _{0}^{x}t^{a-1}\,(1-t)^{b-1}\,dt$.

При $x=1$ неповна бета-функція збігається з повною.

Регуляризована неповна бета-функція визначається через повну і неповну бета-функції:

$I_{x}(a,\;b)={\frac {\mathrm {B} _{x}(a,\;b)}{\mathrm {B} (a,\;b)}}$.

Властивості $I(x)$

$I_{0}(a,\;b)=0$;

$I_{1}(a,\;b)=1$;

$I_{x}(a,\;b)=1-I_{1-x}(b,\;a)$.

Див. також

• Гамма-функція
• Невластивий інтеграл
• Інтеграл Рімана
• Інтегральне числення

Джерела

• Підкуйко, Сергій (2004). Математичний аналіз — Т.1. Множини. Дійсні числа. Границя послідовності. Границя функції. Неперервність функції. Диференціальне числення функцій однієї змінної. Львів: Галицька видавнича спілка. с. 530. ISBN 966-7893-26-Х. {{cite book}}: Перевірте значення |isbn=: недійсний символ (довідка)
• Григорій Михайлович Фіхтенгольц. Курс диференціального та інтегрального числення. — 2024. — 2200+ с.(укр.)