Алгоритм пошуку

Алгоритм пошуку — алгоритм, який вирішує задачу пошуку, тобто, знаходить інформацію, яка зберігається в певній структурі даних. Структури даних можуть бути реалізовані за допомогою зв'язаних списків, масивів, дерев пошуку, хеш-таблиць чи інших методів зберігання інформації. Алгоритм пошуку на пряму залежить від структури даних, для якої він реалізований. Дуже часто алгоритм пошуку налічує особливі команди які задають структуру даних, наприклад SQL SELECT.^[1]^[2]

Опис

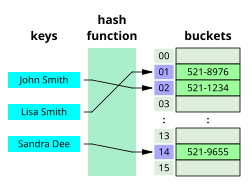
Алгоритми пошуку класифікуються на основі їх механізму пошуку. Лінійний пошук працює достатньо повільно, відносно бінарного пошуку, але на практиці часто зустрічається. Алгоритм лінійного пошуку порівнює кожний елемент в структурі даних зі значенням котре потрібно знайти. Існує також бінарний пошук, або половинно-інтервальний пошук, однак він працює лише з відсортованими елементами, один з найшвидших алгоритмів, який повторно порівнює пошуковий елемент з центральним елементом заданої структури, якщо знайшов то кінець, якщо ні, то порівнює елементи та продовжує пошук в лівій чи правій частині структури даних поки не знайде потрібний. Реалізація алгоритму пошуку для хеш-таблиці — складне завдання, бо в такій структурі даних кожному елементу відповідає певний ключ (key), та данні відсортовані по цим ключам.^[3] Потрібно досить гарно реалізувати хеш-функцію для пошуку елементу по ключу,^[4] бо алгоритм пошуку буде шукати спочатку ключ, а потім отримуватиме значення по ключу.

Алгоритми пошуку оцінюються на основі їх складності чи максимального часу виконання. Бінарний пошук має максимальну складність $\mathrm {O} (\log(n))$ , або логарифмічний час виконання. Це означає, що максимальна кількість операцій, необхідних для пошуку $Cmp_{\max }=\log _{2}n$ , де $n$ — кількість елементів.

Реалізація бінарного пошуку, псевдокод:

BinarySearch(A[0..N-1], value, low, high) {
     if (high < low)
         return -1; // не знайдено
     mid = (low + high) / 2;
     if (A[mid] > value) 
         return BinarySearch(A, value, low, mid-1); рекурсивно обходимо праву частину масива
     else if (A[mid] < value)
         return BinarySearch(A, value, mid+1, high); рекурсивно обходимо ліву частину масива
     else
         return mid; // знайдено
   }

Класифікація

Віртуально — просторий пошук

Алгоритми пошуку віртуальних просторів використовуються в задачах, де мета полягає в тому, щоб знайти набір значень певних змінних, які будуть задовольняти конкретні математичні рівняння чи нерівності. Вони також використовуються, коли треба знайти призначення змінної, яка буде максимізувати або мінімізувати деяку функцію цих змінних. Алгоритми включають в себе основний пошук «грубою силою» («наївний» пошук), а також різні евристики, які намагаються використовувати часткове знання структур простору, таких як лінійна релаксація, обмежені генерації чи обмежені поширення.

Важливим підкласом є локальний пошуковий метод, який розглядає елементи простору пошуку як вершини графу з ребрами, визначені за допомогою набору евристик, сканує простір шляхом переходу від одного пункту до іншого. Ця категорія включає в себе велику різноманітність загальних метаевристичних методів, таких як алгоритм імітації відпалу, tabu пошук, A-teams, які поєднують в собі довільні евристики певним чином.

Цей клас також включає в себе різні алгоритми пошуку дерева, що задає елементи як вершини дерева та обходить дерево в особливому порядку. Такий алгоритм включає в себе вичерпні методи, такі як пошук у глибину, пошук у ширину, а також різні евристичні методи, засновані на деревах пошуку. Дерева пошуку гарантовано знайде точне чи оптимальне рішення за невеликий проміжок часу.

Інший важливий підклас це алгоритми для вивчення дерева ігор, таких як шахи або нарди, вузли дерева задають усіх можливі ситуації гри, які можуть виникнути. Мета такого алгоритму є знаходження ходу, котрий забезпечить перемогу, беручи до уваги всі можливі ходи під час гри. Аналогічні проблеми виникають, коли людина або машина повинна виконати послідовне рішення, наприклад, в роботі керівництва, фінансах або плануванні військової стратегії. Такий рід проблем як комбінаторний пошук широко вивчається в штучному інтелекті. Приклади алгоритмів для цього класу:

Підструктур даної структури

Назва «комбінаторний пошук», як правило, використовуються для алгоритмів, які реалізовані для конкретної підструктури заданої дискретної структури. Термін комбінаторна оптимізація, як правило, використовується, коли мета полягає в тому, щоб знайти підструктуру зі значенням максимального (мінімального) параметра. (Підструктура представлена в комп'ютері за допомогою набору цілочисельних змінних з обмеженнями. Ці проблеми можна розглядати як окремі випадки дискретної оптимізації, але вони формуються та вирішуються у більш абстрактній формі.)

Важливими підкласами є алгоритми графу, зокрема алгоритми обходу графу, для знаходження конкретної структури в даному графі, наприклад підграф. Приклади алгоритмів графу:

Пошук максимуму функції

1953 року американський статистик Джек Кіфер^[en] розробив метод пошуку Фібоначчі, який подібно до алгоритму Грувера, з теоретичної точки зору, є швидшим за лінійний пошук або Метод «грубої сили» навіть без використання знання структури даних або інших евристик. Також пошук Фібоначчі можна використовувати для пошуку максимуму унімодальної функції, і він має багато інших застосувань в області комп'ютерної науки.

Див. також

Примітки

↑ Beame та Fich, 2001, с. 39.
↑ Knuth, 1998, §6.5 ("Retrieval on Secondary Keys").
↑ Knuth, 1998, §6.2 («Searching by Comparison of Keys»).
↑ Knuth, 1998, §6.4, (Hashing).
↑ Kagan E. and Ben-Gal I. A Group-Testing Algorithm with Online Informational Learning. — IIE Transactions, 46:2, 164-184,, 2014. Архівовано з джерела 5 листопада 2016. Процитовано 25 квітня 2017.

Посилання

Алгоритм пошуку [Архівовано 25 лютого 2022 у Wayback Machine.] // ВУЕ

[FOOTNOTEBeameFich200139-1] Beame та Fich, 2001, с. 39.

[FOOTNOTEKnuth1998§6.5_("Retrieval_on_Secondary_Keys")-2] Knuth, 1998, §6.5 ("Retrieval on Secondary Keys").

[FOOTNOTEKnuth1998§6.2_(«Searching_by_Comparison_of_Keys»)-3] Knuth, 1998, §6.2 («Searching by Comparison of Keys»).

[FOOTNOTEKnuth1998§6.4,_(Hashing)-4] Knuth, 1998, §6.4, (Hashing).

[5] Kagan E. and Ben-Gal I. A Group-Testing Algorithm with Online Informational Learning. — IIE Transactions, 46:2, 164-184,, 2014. Архівовано з джерела 5 листопада 2016. Процитовано 25 квітня 2017.

[1]

[2]

[3]

[4]

[5]