Зворотний зв'язок

Зворо́тний зв'язо́к (англ. feedback) — вплив результату функціонування будь-якої системи на характер її подальшого функціонування. Термін «зворотний зв'язок» використовують стосовно перебігу процесів у соціальних, біологічних, технічних, економічних та інших системах, а також у кібернетиці^[1] та теорії автоматичного регулювання та управління.

Одне з перших досліджень впливу зворотного зв'язку на результат функціонування системи було виконане Майклом Фарадеєм у популярній роботі «Історія свічки».

Типи зворотного зв'язку

За характером впливу розрізняють^[2]:

Позитивний та негативний зворотний зв'язок

позитивний зворотний зв'язок впливає на систему таким чином, що збільшує вихідний результат її функціонування. У теорії автоматичного управління позитивний зворотний зв'язок реалізується шляхом передачі на вхід системи частини вихідного сигналу таким чином, що сигнал зворотного зв'язку збігається у фазі з вхідним сигналом, що є еквівалентним збільшенню вхідного сигналу. В окремих випадках позитивний зв'язок може призводити до генерації в системі — коли будь-яка флуктуація в системі передається на її вхід і підсилюється, завдяки чому в системі виникають незатухаючі коливання.

негативний зворотний зв'язок впливає на систему таким чином, що зменшує вихідний результат її функціонування. В теорії автоматичного управління негативний зворотний зв'язок реалізується шляхом передачі на вхід системи частини вихідного сигналу таким чином, що сигнал зворотного зв'язку знаходиться у протифазі з вхідним сигналом, що є еквівалентним зменшенню вхідного сигналу, що призводить до зниження коефіцієнта підсилення системи, але при цьому також підвищується стійкість системи та зменшується похибка та інерційність системи.

Жорсткий та гнучкий (elastic feedback) зворотний зв'язок

жорсткий зворотний зв'язок діє в усталеному і перехідному режимах роботи системи.

гнучкий зворотний зв'язок діє тільки у перехідному режимі роботи системи, несе інформацію про швидкість змін в системі. В теорії автоматичного управління реалізується додаванням в контур зворотного зв'язку диференцюючих елементів.

Загальний та місцевий зворотний зв'язок

загальний зворотний зв'язок формується за рахунок передачі результату функціонування всієї системи на її вхід.

місцевий зворотний зв'язок формується за рахунок передачі результату функціонування окремої ланки системи на вхід цієї ланки.

Крім того, у САР розрізняють зовнішній зворотний зв'язок, який з'єднує вихід усієї системи з її входом, та внутрішній (місцевий), що з'єднує вихід окремого елемента або групи послідовно з'єднаних елементів з їх входом.

Математичне формулювання

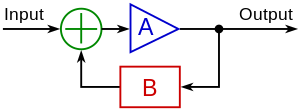
Нехай вхідний сигнал u та вихідний сигнал U певного об'єкта (чорної скриньки) зв'язано лінійним співвідношенням

U=ku\,

,

де k — коефіцієнт підсилення.

Якщо на вхід системи подати крім сигналу u ще й частково сигнал з виходу, так що загальний вхідний сигнал стане $u+\alpha U$ , де $\alpha$ — певний коефіцієнт зворотного зв'язку, то отримаємо

U=k(u+\alpha U)\,

.

У такому разі вихідний сигнал визначатиметься формулою

U={\frac {ku}{1-k\alpha }}

.

При додатних значеннях α вихідний сигнал посилюватиметься, але стабільність падатиме. При α = 1/k вихідний сигнал стане нескінченно великим (насправді в такому разі система вийде з лінійного режиму).

При від'ємних значеннях α підсилення зменшується й система стабілізується.

Див. також

Примітки

↑ Архівована копія. Архів оригіналу за 15 січня 2012. Процитовано 30 травня 2009.{{cite web}}: Обслуговування CS1: Сторінки з текстом «archived copy» як значення параметру title (посилання)
↑ Велика Радянська Енциклопедія^{[недоступне посилання з липня 2019]}

Література

М. Г. Попович, О. В. Ковальчук. Теорія автоматичного керування: Підручник. — 2-ге вид. — К.: Либідь, 2007. — 656 с.
Л. фон Берталанфи «Общая теория систем — критический обзор»
Папушин Ю. Л., Білецький В. С. Основи автоматизації гірничого виробництва. — Донецьк : Східний видавничий дім, 2007. — 168 с. — ISBN 978-966-317-004-6.
Іванов А. О. Теорія автоматичного керування: Підручник. — Дніпропетровськ: Національний гірничий університет. — 2003. — 250 с.
Енциклопедія кібернетики. тт. 1, 2. — К.: Головна редакція УРЕ, 1973. — 584 с.

[1] Архівована копія. Архів оригіналу за 15 січня 2012. Процитовано 30 травня 2009.{{cite web}}: Обслуговування CS1: Сторінки з текстом «archived copy» як значення параметру title (посилання)

[2] Велика Радянська Енциклопедія^{[недоступне посилання з липня 2019]}

[1]

[2]