Регуляризація (математика)

Регуляризація, в математиці і статистиці, а також в задачах машинного навчання і обернених задачах, означає додавання деякої додаткової інформації, щоб знайти рішення некоректно поставленої задачі, або щоб уникнути перенавчання.

Обидві функції точно описують експериментальні точки з нульовою похибкою. Навчена модель може бути схильна вибирати зелену функцію, що може бути ближчою до справжньої невідомої функції розподілу, за допомогою $\lambda$, ваги регуляризуючого виразу.

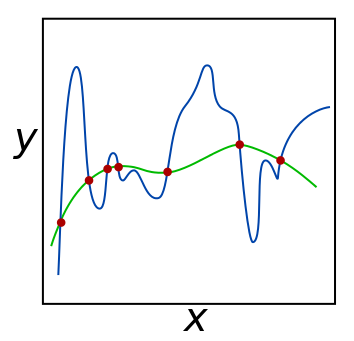
Використання регуляризації для класифікації

Регуляризацію використовують у задачах класифікації. Емпіричне навчання класифікаторів на скінченному набору даних завжди є недостатньо визначеною задачею, бо в загальному випадку ми намагаємось вивести функцію від довільного $x$ по декільком заданим прикладам $x_{1},x_{2},...x_{n}$.

Загалом регуляризуючий вираз $R(f)$ додається до функції втрат:

$\min _{f}\sum _{i=1}^{n}V(f({\hat {x}}_{i}),{\hat {y}}_{i})+\lambda R(f),$

де $V$ — функція, що визначає похибку передбачення $f(x)$ для значень $y$, (наприклад, квадрати похибок), а параметр $\lambda$ визначає важливість доданка для регуляризації. Зазвичай $R(f)$ визначається як штраф за складність функції $f$. Зокрема, поняття складності включає обмеження на гладкість та на норму векторного простору.

Фактично, процедура регуляризації є спробою застосувати лезо Оккама до рішення (див. малюнок вище). З точки зору баєсового висновування, багато технік регуляризації є накладанням обмежень на апріорний вигляд розподілу параметрів моделі.

Узагальнення

Регуляризація може використовуватись як спосіб покращення узагальнення для моделі у машинному навчанні.

Основна задача машинного навчання полягає в тому, щоб знайти функцію, сумарна похибка передбачень якої для всіх можливих значень була б мінімальною. Очікувана похибка$f_{n}$ виражається як:

$I[f_{n}]=\int _{X\times Y}V(f_{n}(x),y)\rho (x,y)\,dx\,dy$

Зазвичай в таких задачах лише частина усіх можливих даних, частково зашумлених, є доступною для навчання. Таким чином, очікувана похибка є необчислюваною величиною, і найкраще наближення — це емпірична похибка, що вираховується на базі $N$ доступних зразків:

$I_{S}[f_{n}]={\frac {1}{n}}\sum _{i=1}^{N}V(f_{n}({\hat {x}}_{i}),{\hat {y}}_{i})$

Без обмежень складності функціонального простору, в якому проводиться пошук, модель може бути навчена так, щоб відповідна їй функція проходила через кожну точку наявних даних $x_{i}$. Але якщо значення $x_{i}$ містять шум, то модель може "страждати" від перенавчання і видавати погані значення очікуваних помилок. Регуляризація вводить штраф за включення зайвих областей функціонального простору, що використовується для побудови моделі і це може покращити узагальнення.

Регуляризація Тихонова

При навчанні лінійною функцією, такою як $f(x)=w\cdot x$, в якій $w$ шуканий вектор, $L_{2}$-норма функції втрат відповідає регуляризації Тихонова. Ця, одна з найбільш використовуваних форм регуляризації, виражається як:

$\min _{w}\sum _{i=1}^{n}V({\hat {x}}_{i}\cdot w,{\hat {y}}_{i})+\lambda \|w\|_{2}^{2}$

У випадку загальної функції, ми беремо норму функції у її гільбертовому просторі з відтворювальним ядром:

$\min _{f}\sum _{i=1}^{n}V(f({\hat {x}}_{i}),{\hat {y}}_{i})+\lambda \|f\|_{\mathcal {H}}^{2}$

Оскільки норма $L_{2}$ диференційовна, то проблема навчання з використанням регуляризації Тихонова, може бути розв'язана градієнтним спуском.

Регуляризація Тихонова для методу найменших квадратів

Навчання з функцією втрат, вираженою методом найменших квадратів і регуляризація Тихонова можна розв'язати аналітично. 

$\min _{w}{\frac {1}{n}}({\hat {X}}w-{\hat {Y}})^{2}+\lambda \|w\|_{2}^{2}$

$\nabla _{w}={\frac {2}{n}}{\hat {X}}^{T}({\hat {X}}w-{\hat {Y}})+2\lambda w$ $\leftarrow$ необхідна умова екстремуму

$0={\hat {X}}^{T}({\hat {X}}w-{\hat {Y}})+n\lambda w$

$w=({\hat {X}}^{T}{\hat {X}}+\lambda nI)^{-1}({\hat {X}}^{T}{\hat {Y}})$

Відповідно до оптимізаційної задачи, інші значення $w$ будуть давати більші значення для функції втрат. Це можна перевірити за допомогою другої похідної $\nabla _{ww}$.

Цей алгоритм потребує $O(d^{3}+nd^{2})$ часу для тренування. Доданками тут є час на пошук зворотньої матриці і на обчислення $X^{T}X$, відповідно. Перевірка займає час $O(nd)$.

Рання зупинка

Рання зупинка може бути розглянута як регуляризація в часі. Загалом, такі методики як градієнтний спуск, мають тенденцію до створення все більш і більш складних функцій з часом. За допомогою регуляризації в часі складність моделі може контролюватися. 

На практиці, для впровадження цієї методики, використовується додатковий валідаційний масив даних, статистично незалежний від того, що використовується для тренування. Модель тренується до тих пір, доки результативність на валідаційному масиві не перестає зростати. Після цього модель тестується на тестовому масиві.

Див. також

• Виключення (нейронні мережі)

Посилання

• A. Neumaier, Solving ill-conditioned and singular linear systems: A tutorial on regularization, SIAM Review 40 (1998), 636—666. Available in pdf from author's website.
• Rosasco, L. Regularized Least Squares, Class Notes from MIT 9.520. Link
• L. Rosasco, T. Poggio, A Regularization Tour of Machine Learning, MIT-9.520 Lectures Notes (book draft), 2015.
• Rosasco, L. Early Stopping, Class Notes from MIT 9.520. http://www.mit.edu/~9.520/fall15/Classes/early_stopping.html
• Rosasco, L. Sparsity, Class Notes from MIT 9.520. http://www.mit.edu/~9.520/fall15/Classes/sparsity.html
• Rosasco, L. Proximal Methods, Class Notes from MIT 9.520. http://www.mit.edu/~9.520/fall15/Classes/proxy.html