Вікіпедія

Коловий граф

граф перетинів множини хорд кола

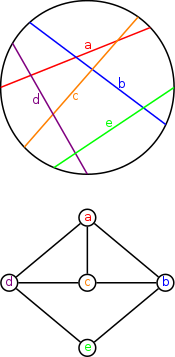
У теорії графів коловий граф — це граф перетинів множини хорд кола. Тобто це неорієнтований граф, вершини якого можна ототожнити з хордами кола, і ці вершини суміжні тоді й тільки тоді, коли відповідні хорди перетинаються.

Коло з п'ятьма хордами і відповідний коловий граф

Алгоритмічна складність ред.

Спінрад[1] представив алгоритм, який працює за час O(n2), який перевіряє, чи є заданий неорієнтований граф з n вершинами коловим, і якщо він коловий, будує множину хорд, які дають коловий граф.

Багато інших задач, які NP-повні на графах загального вигляду, мають алгоритми поліноміального часу, якщо обмежитися коловими графами. Наприклад, Клокс[2] показав, що деревну ширину колового графа можна визначити, а оптимальне дерево декомпозиції побудувати за час O(n3). Крім того, найменше заміщення (тобто хордальний граф з якомога меншим числом ребер, що містить даний коловий граф як підграф) можна знайти за час O(n3)[3]. Тіскін[4] показав, що найбільшу кліку колового графа можна знайти за час O(n log2 n), а Неш і Грегг[5] показали, що найбільшу незалежну множину незваженого колового графа можна знайти за час O(n min{d, α}), де d — параметр графа, відомий як щільність, а α — число незалежності колового графа.

Все ж є задачі, які залишаються NP-повними, навіть якщо обмежитися коловими графами. До цих задач належать пошуки домінівної множини, найменшої зв'язної домінівної множини і найменшої тотальної домінівної множини[6].

Хроматичне число ред.

 
Хорди, що утворюють граф Агеєва, вільний від трикутників коловий граф з 220 вершинами і хроматичним числом 5[7], поданий у вигляді конфігурації прямих на гіперболічній площині

Хроматичне число колового графа дорівнює найменшому числу кольорів, які можна використати для розфарбовування хорд, так, щоб ніякі дві перетинні хорди не мали однакового кольору. Оскільки можна утворити коловий граф, у якому довільна велика множина хорд перетинають одна одну, хроматичне число колового графа може бути довільно великим, а визначення хроматичного числа колового графа є NP-повною задачею[8]. NP-повною задачею є й перевірка, чи можна розфарбувати коловий граф чотирма кольорами[9]. Унгер[10] стверджував, що пошук розфарбування трьома кольорами можна здійснити за поліноміальний час, але в описі його результатів відсутні багато подробиць[10].

Деякі автори досліджували задачу розфарбовування обмежених підкласів колових графів малим числом кольорів. Зокрема, колові графи, в яких немає множин з k і більше хорд, в яких всі хорди перетинають одна одну, можна розфарбувати, не перевищуючи   кольорів[11]. Зокрема, при k = 3 (тобто для колових графів без трикутників) хроматичне число не перевищує п'яти, і ця межа точна — всі колові графи без трикутників можна розфарбувати в п'ять кольорів і існують колові графи без трикутників, що вимагають п'яти кольорів для розфарбовування[12]. Якщо коловий граф має обхват щонайменше п'ять (тобто в ньому немає трикутників і циклів з чотирма вершинами), його можна розфарбувати, обмежившись трьома кольорами[13]. Задача розфарбовування рамкових графів без трикутників еквівалентна задачі подання рамкових графів у вигляді графа, ізометричного прямому добутку дерев. У цій відповідності задач число кольорів у розфарбуванні відповідає числу дерев у добутку[14].

Застосування ред.

Колові графи з'являються під час проєктування НВІС як абстракція окремого випадку трасування друкованих плат, відомого як «двополюсне трасування перетинів каналів». У цьому випадку ділянка трасування є прямокутником, усі мережі є двополюсниками, а виводи розташовуються по периметру прямокутника. Легко бачити, що граф перетинів цієї мережі є коловим графом[15]. Одна з цілей трасування — забезпечення відсутності електричного контакту між різними мережами та розташування можливих перетинних частин на різних шарах. Таким чином, колові графи охоплюють частину задач трасування.

Розфарбування колових графів можна використовувати також для пошуку книжкового вкладення довільних графів — якщо вершини заданого графа G розташовані на колі, а ребра графа G утворюють хорди кола, то граф перетинів цих хорд є коловим графом, а розфарбування цього колового графа еквівалентне книжковому вкладенню, що зберігає колове розташування. У цій еквівалентності число кольорів відповідає числу сторінок у книжковому вкладенні[9].

Пов'язані класи графів ред.

Граф перетинів множини інтервалів на прямій називається інтервальним графом.

Граф є коловим тоді і тільки тоді, коли він є правильним інтервальним графом. Це графи, вершини яких відповідають (відкритим) відрізкам на прямий і дві вершини з'єднані ребром, якщо два інтервали мають непорожній перетин. При цьому ніякий інтервал не міститься повністю в іншому інтервалі.

Струнні графи, графи перетинів кривих на площині, включають колові графи як окремий випадок.

Будь-який дистанційно-успадковуваний граф є коловим графом, як і будь-який граф перестановки або індиферентний граф. Будь-який зовніпланарний граф також є коловим[16][9].

Примітки ред.

  1. ↑ Spinrad, 1994.
  2. ↑ Kloks, 1996.
  3. ↑ Kloks, Kratsch, Wong, 1998.
  4. ↑ Tiskin, 2010.
  5. ↑ Nash, Gregg, 2010.
  6. ↑ Keil, 1993.
  7. ↑ Ageev, 1996.
  8. ↑ Garey, Johnson, Miller, Papadimitriou, 1980.
  9. ↑ а б в Unger, 1988.
  10. ↑ а б Unger, 1992.
  11. ↑ (Černý, 2007). Для более ранних границ см. (Gyárfás, 1985), (Косточка, 1988) и (Kostochka, Kratochvíl, 1997).
  12. ↑ См. (Косточка, 1988) для верхней границы и (Ageev, 1996) графов, достигающих нижнюю границу. Карапетян (Карапетян, 1984) и (Gyárfás, Lehel, 1985) указали ранее более слабые границы для той же задачи.
  13. ↑ Ageev, 1999.
  14. ↑ Bandelt, Chepoi, Eppstein, 2010.
  15. ↑ Sherwani, 2000.
  16. ↑ Wessel, Pöschel, 1985.

Література ред.

  • A. A. Ageev. A triangle-free circle graph with chromatic number 5 // Discrete Mathematics. — 1996. — Т. 152, вип. 1-3 (11 квітня). — С. 295–298. — DOI:10.1016/0012-365X(95)00349-2.
  • A. A. Ageev. Every circle graph of girth at least 5 is 3-colourable // Discrete Mathematics. — 1999. — Т. 195, вип. 1-3 (11 квітня). — С. 229–233. — DOI:10.1016/S0012-365X(98)00192-7.
  • H.-J. Bandelt, V. Chepoi, D. Eppstein. Combinatorics and geometry of finite and infinite squaregraphs // SIAM Journal on Discrete Mathematics. — 2010. — Т. 24, вип. 4 (11 квітня). — С. 1399–1440. — arXiv:0905.4537. — DOI:10.1137/090760301.
  • Jakub Černý. Coloring circle graphs // Electronic Notes in Discrete Mathematics. — 2007. — Т. 29 (11 квітня). — С. 357–361. — DOI:10.1016/j.endm.2007.07.072.
  • M. R. Garey, D. S. Johnson, G. L. Miller, C. Papadimitriou. The complexity of coloring circular arcs and chords // SIAM. J. on Algebraic and Discrete Methods. — 1980. — Т. 1, вип. 2 (11 квітня). — С. 216–227. — DOI:10.1137/0601025.
  • A. Gyárfás. On the chromatic number of multiple interval graphs and overlap graphs // Discrete Mathematics. — 1985. — Т. 55, вип. 2 (11 квітня). — С. 161–166. — DOI:10.1016/0012-365X(85)90044-5.. Як процитовано в Агеєва (Ageev, 1996)
  • A. Gyárfás, J. Lehel. Covering and coloring problems for relatives of intervals // Discrete Mathematics. — 1985. — Т. 55, вип. 2 (11 квітня). — С. 167–180. — DOI:10.1016/0012-365X(85)90045-7.. Як процитовано в Агеєва (Ageev, 1996)
  • И. А. Карапетян. О совершенных дуговых и хордовых графах. — Новосибирск : Институт математики, 1984. — (Автореферат диссертации канд. Физ-матю наук: 01.01.09)
  • J. Mark Keil. The complexity of domination problems in circle graphs // Discrete Applied Mathematics. — 1993. — Т. 42, вип. 1 (11 квітня). — С. 51–63. — DOI:10.1016/0166-218X(93)90178-Q.
  • Ton Kloks. Treewidth of Circle Graphs // Int. J. Found. Comput. Sci.. — 1996. — Т. 7, вип. 2 (11 квітня). — С. 111–120. — DOI:10.1142/S0129054196000099.
  • T. Kloks, D. Kratsch, C. K. Wong. Minimum fill-in on circle and circular-arc graphs // Journal of Algorithms. — 1998. — Т. 28, вип. 2 (11 квітня). — С. 272–289. — DOI:10.1006/jagm.1998.0936.
  • А. В. Косточка. Модели и методы оптимизации / В. Т. Дементьев. — 1988. — Т. 10. — С. 204–226. — (Труды Института математики) — ISBN 5-02-028584-6, ББК В1я54 + В18я54.
  • A.V. Kostochka, J. Kratochvíl. Covering and coloring polygon-circle graphs // Discrete Mathematics. — 1997. — Т. 163, вип. 1–3 (11 квітня). — С. 299–305. — DOI:10.1016/S0012-365X(96)00344-5.
  • Nicholas Nash, David Gregg. An output sensitive algorithm for computing a maximum independent set of a circle graph // Information Processing Letters. — 2010. — Т. 116, вип. 16 (11 квітня). — С. 630–634. — DOI:10.1016/j.ipl.2010.05.016.
  • Jeremy Spinrad. Recognition of circle graphs // Journal of Algorithms. — 1994. — Т. 16, вип. 2 (11 квітня). — С. 264–282. — DOI:10.1006/jagm.1994.1012.
  • Alexander Tiskin. Proceedings of ACM-SIAM SODA 2010. — 2010. — С. 1287–1296.
  • Walter Unger. STACS 88: 5th Annual Symposium on Theoretical Aspects of Computer Science, Bordeaux, France, February 11–13, 1988, Proceedings. — Berlin : Springer, 1988. — Т. 294. — С. 61–72. — (Lecture Notes in Computer Science) — DOI:10.1007/BFb0035832.
  • Walter Unger. STACS 92: 9th Annual Symposium on Theoretical Aspects of Computer Science, Cachan, France, February 13–15, 1992, Proceedings. — Berlin : Springer, 1992. — Т. 577. — С. 389–400. — (Lecture Notes in Computer Science) — DOI:10.1007/3-540-55210-3_199.
  • W. Wessel, R. Pöschel. Graphs, Hypergraphs and Applications: Proceedings of the Conference on Graph Theory Held in Eyba, October 1st to 5th, 1984. — B.G. Teubner, 1985. — Т. 73. — С. 207–210. — (Teubner-Texte zur Mathematik). Як процитовано в (Unger, 1988).
  • Naveed Sherwani. Algorithms for VLSI Physical Design Automation. — Boston/Dordrecht/London : Kluwer Academic Publishers, 2000. — ISBN 0-7923-8393-1.

Посилання ред.

  • Circle graph. Архів оригіналу за 29 червня 2021. Процитовано 25 червня 2021.
Отримано з https://uk.wikipedia.org/w/index.php?title=Коловий_граф&oldid=36304642