Бент-функція

Бент-функція (від англ. bent — вигнутий, нахилений^[1]^[2]) — булева функція з парним числом змінних, для якої відстань Геммінга від множини афінних булевих функцій з тим самим числом змінних найбільша. Бент-функції в цьому сенсі мають найбільший ступінь нелінійності серед усіх функцій з даним числом змінних і завдяки цьому широко застосовуються в криптографії для створення шифрів, максимально стійких до методів лінійного та диференціального криптоаналізу^[1].

Близьким за змістом є термін «максимально нелінійна функція», кількість змінних таких функцій не обмежується парними числами. Максимально нелінійна функція з парною кількістю змінних є бент-функцією^[1].

Визначення

Відстань Геммінга для двох булевих функцій $n$ змінних — кількість відмінностей у значеннях цих функцій на повній множині $2 n$ наборів змінних.

Афінна (лінійна) булева функція — булева функція, поліном Жегалкіна якої не має нелінійних членів, тобто членів, що є кон'юнкцією декількох змінних.

Ступінь нелінійності булевої функції $deg (f)$ — число змінних у найдовшому доданку її полінома Жегалкіна.

Нелінійність булевої функції $N (f)$ — відстань Геммінга від даної функції до множини всіх афінних функцій.

Історія

Бент-функції запровадив у 1960-х роках Оскар Ротгауз (1927—2003), який тоді (від 1960 до 1966 року) працював у Інституті оборонного аналізу^[en] (IDA), де займався криптографічними дослідженнями. Його перша робота з бент-функцій відноситься до 1966 року^[3], проте вона була засекречена й у відкритій пресі з'явилася тільки 1976 року^[4].

У 1960-х роках В. А. Єлісєєв та О. П. Степченков досліджували бент-функції в СРСР, проте їхні роботи досі засекречено^[1]. Відомо, що вони називали бент-функції «мінімальними функціями» і запропонували побудову Макфарланда ще 1962 року.

Властивості

Нелінійність бент-функцій із кількістю змінних $n$ ( $n$ — парне) визначається співвідношенням^[1]^[2]:

N(f)=2^{n-1}-2^{{\frac {n}{2}}-1}

.

Для максимально нелінійних функцій з непарним числом змінних точного виразу нелінійності невідомо^[1].

Приклади бент-функцій

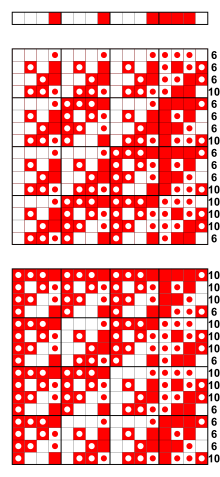
Нижче наведено приклади бент-функцій чотирьох, шести та восьми змінних^[5].

n=4:f_{1}(X)=x_{1}x_{3}\oplus x_{2}x_{4};N(f_{1})=6;

n=6:f_{2}(X)=x_{1}x_{2}x_{3}\oplus x_{1}x_{4}\oplus x_{2}x_{5}\oplus x_{3}x_{6};N(f_{2})=28;

n=8:f_{3}(X)=x_{1}x_{2}x_{3}\oplus x_{2}x_{4}x_{5}\oplus x_{1}x_{2}\oplus x_{1}x_{4}\oplus x_{2}x_{6}\oplus x_{3}x_{5}\oplus x_{4}x_{5}\oplus x_{7}x_{8};N(f_{3})=120;

n=8:f_{4}(X)=x_{1}x_{2}x_{3}\oplus x_{2}x_{4}x_{5}\oplus x_{3}x_{4}x_{6}\oplus x_{1}x_{4}\oplus x_{2}x_{6}\oplus x_{3}x_{4}\oplus x_{3}x_{5}\oplus x_{3}x_{6}\oplus x_{4}x_{5}\oplus x_{4}x_{6}\oplus x_{7}x_{8};N(f_{4})=120.

Монографія

У книзі^[1] наведено докладний огляд результатів у галузі бент-функцій. Розглянуто історію відкриття бент-функцій, описано їх застосування в криптографії та дискретній математиці. Досліджуються основні властивості та еквівалентні подання бент-функцій, класифікації бент-функцій від малої кількості змінних, комбінаторні та алгебричні побудови бент-функцій, зв'язок бент-функцій з іншими криптографічними властивостями. Вивчаються відстані між бент-функціями та група автоморфізмів бент-функцій. Розглянуто верхні та нижні оцінки числа бент-функцій та гіпотези про його асимптотичне значення. Наведено докладний систематичний огляд 25 різних узагальнень бент-функцій, розглянуто відкриті питання в цій галузі. Книга^[1] 2015 року містить понад 125 теорем про бент-функції та суттєво розширює книгу^[2], опубліковану 2011 року.

Примітки

↑ ^а ^б ^в ^г ^д ^е ^ж ^и N. Tokareva. Bent functions: results and applications to cryptography : [англ.] // Acad. Press. Elsevier, 2015. 220 pages. : журнал.
↑ ^а ^б ^в Токарева Н. Н. Нелинейные булевы функции: бент-функции и их обобщения [Архівовано 2012-07-14 у Wayback Machine.] // Издательство LAP LAMBERT Academic Publishing (Saarbrucken, Germany), 2011. ISBN 978-3-8433-0904-2. 180 с.
↑ Rothaus O. On bent functions // IDA CRD W.P. No. 169. 1966.
↑ O. S. Rothaus. On "Bent" Functions : [англ.] // Journal of Combinatorial Theory, Series A : журнал. — 1976. — Vol. 20, № 3 (May). — С. 300—305. — ISSN 0097-3165. — DOI:10.1016/0097-3165(76)90024-8.
↑ Молдовян А. А. Криптография. Скоростные шифры // БХВ-Петербург, 2002. ISBN 594157214X, ISBN 9785941572144. 496 c.

[Tokareva2015-1] а ^б ^в ^г ^д ^е ^ж ^и N. Tokareva. Bent functions: results and applications to cryptography : [англ.] // Acad. Press. Elsevier, 2015. 220 pages. : журнал.

[Tokareva2011-2] а ^б ^в Токарева Н. Н. Нелинейные булевы функции: бент-функции и их обобщения [Архівовано 2012-07-14 у Wayback Machine.] // Издательство LAP LAMBERT Academic Publishing (Saarbrucken, Germany), 2011. ISBN 978-3-8433-0904-2. 180 с.

[Rothaus1966-3] Rothaus O. On bent functions // IDA CRD W.P. No. 169. 1966.

[Rothaus1976-4] O. S. Rothaus. On "Bent" Functions : [англ.] // Journal of Combinatorial Theory, Series A : журнал. — 1976. — Vol. 20, № 3 (May). — С. 300—305. — ISSN 0097-3165. — DOI:10.1016/0097-3165(76)90024-8.

[Moldovan2002-5] Молдовян А. А. Криптография. Скоростные шифры // БХВ-Петербург, 2002. ISBN 594157214X, ISBN 9785941572144. 496 c.

[1]

[2]

[3]

[4]

[5]