Алгоритм Грехема

Алгоритм Грехема (англ. Graham scan) — метод знаходження опуклої оболонки для скінченної множини точок на площині за час O(n log n). Названий на честь Рональда Грехема, який опублікував первісний варіант алгоритму в 1972 році^[1]. Алгоритм знаходить всі вершини опуклої оболонки впорядковані вздовж її межі.

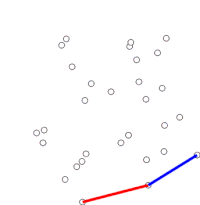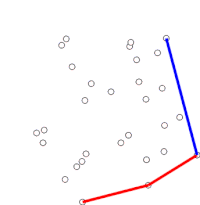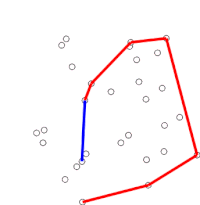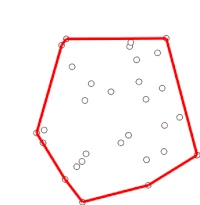
Приклад знаходження опуклої оболонки алгоритмом Грехема.

Алгоритм ред.

Як можна побачити, A — B і B — C слідують в напрямку протилежному годинниковому, а C — D ні. Алгоритм визначає таку ситуацію та відміняє попередньо обраний сегмент доти, доки напрямок знов не буде проти годинникового (B — D в цьому випадку.)

Перший крок в алгоритмі — знайти точку з найменшою у-координатою. Якщо таких декілька, то обираємо серед них точку з найменшою х-координатою. Назвемо її P. Цей крок має складність O(n), де n — кількість точок. Додамо цю точку в стек.

Далі, точки мають бути відсортовані в порядку зростання кута, який вони разом з P утворюють з віссю х. Будь-який алгоритм сортування підходить. Для пришвидшення обчислень, не обов'язково визначати кут, що ці точки утворюють з віссю х; замість цього достатньо обчислити котангенс цього кута: це монотонно спадна функція на проміжку $[0,\pi ]$ і може бути обчислена простими арифметичними операціями.

Алгоритм виконується вважаючи, що точки відсортовано згідно з попереднім кроком. Для кожної точки він визначає чи було пересування від двох попередніх точок до цієї точки поворотом ліворуч чи поворотом праворуч. Якщо це був поворот праворуч, тоді передостання точка (від якої повертали) не є частиною опуклої оболонки і має бути видалена зі стека. Цей процес триває доти доки останні три точки утворюють поворот праворуч. Як тільки поворот ліворуч був отриманий, алгоритм рухається до наступної точки у відсортованному масиві. (Якщо в якийсь момент виявляється, що три точки колінеарні, користувач може сам вирішувати, що робити в такому випадку, адже іноді потрібно отримати всі точки, що належать до опуклої оболонки.)

Визначення, коли три точки утворюють поворот ліворуч, а коли поворот праворуч не вимагає обчислення кута між двома відрізками, і може бути визначено за допомогою простих арифметичних операцій. Для трьох точок $(x_{1},y_{1})$ , $(x_{2},y_{2})$ і $(x_{3},y_{3})$ , просто обчисліть напрямок векторного добутку двох векторів визначених точками $(x_{1},y_{1})$ , $(x_{2},y_{2})$ і $(x_{1},y_{1})$ , $(x_{3},y_{3})$ , яке характеризується знаком виразу $(x_{2}-x_{1})(y_{3}-y_{1})-(y_{2}-y_{1})(x_{3}-x_{1})$ . Якщо результат 0, точки колінеарні; якщо позитивний, точки утворюють поворот ліворуч, інакше поворот праворуч.

Насамкінець алгоритм досягне точки з якої ми починали, тепер він завершився і стек містить точки опуклої оболонки в напрямку зворотному до годинникового.

Час роботи ред.

Загальний час роботи дорівнює O(n log n).

Псевдокод ред.

# Три точки йдуть проти годинникової стрілки якщо ccw > 0, за стрілкою якщо
# ccw < 0, і колінеарні якщо ccw = 0 через те, що ccw визначена як
# така, що повертає signed area трикутника сформованного p1, p2 та p3.
function ccw(p1, p2, p3):
    return (p2.x - p1.x)*(p3.y - p1.y) - (p2.y - p1.y)*(p3.x - p1.x)

Результат буде збережений в points.

let N           = number of points
let points[N+1] = the array of points
swap points[1] with the point with the lowest y-coordinate
sort points by polar angle with points[1]

# points[0] буде позначкою зупинки алгоритму.
let points[0] = points[N]

# M буде вказувати кількість точок в опуклій оболонці.
let M = 2
for i = 3 to N:
    # Шукаємо наступну правильну точку на опуклій оболонці.
    while ccw(points[M-1], points[M], points[i]) <= 0:
       M -= 1

    # Пересуваємо points[i] в правильне місце та оновлюємо M.
    M += 1
    swap points[M] with points[i]