RSA
RSA (абревіатура від прізвищ Rivest, Shamir та Adleman) — криптографічний алгоритм з відкритим ключем, що базується на обчислювальній складності задачі факторизації великих цілих чисел.
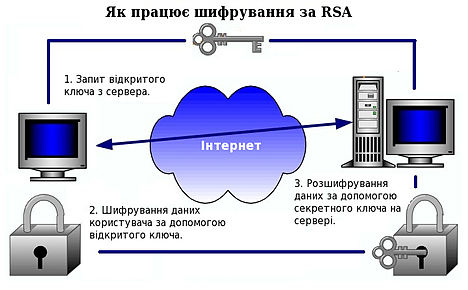
RSA став першим алгоритмом такого типу, придатним і для шифрування, і для цифрового підпису. Алгоритм застосовується до великої кількості криптографічних застосунків.
Історія ред.
Опис RSA було опубліковано у 1977 році Рональдом Райвестом, Аді Шаміром і Леонардом Адлеманом з Массачусетського технологічного інституту (MIT).
Британський математик Кліфорд Кокс[en] (англ. Clifford Cocks), що працював в центрі урядового зв'язку (GCHQ) Великої Британії, описав аналогічну систему в 1973 році у внутрішніх документах центру, але ця робота не була розкрита до 1997 року, тож Райвест, Шамір і Адлеман розробили RSA незалежно від роботи Кокса.
В 1983 році був виданий патент 4405829 [Архівовано 16 жовтня 2007 у Wayback Machine.] США, термін дії якого минув 21 вересня 2000 року.
Опис алгоритму ред.
| Вікіпідручник має книгу на тему |
Алгоритм RSA складається з 4 етапів: генерації ключів, шифрування, розшифрування та розповсюдження ключів.
Безпека алгоритму RSA побудована на принципі складності факторизації цілих чисел. Алгоритм використовує два ключі — відкритий (public) і секретний (private), разом відкритий і відповідний йому секретний ключі утворюють пари ключів (keypair). Відкритий ключ не потрібно зберігати в таємниці, він використовується для шифрування даних. Якщо повідомлення було зашифровано відкритим ключем, то розшифрувати його можна тільки відповідним секретним ключем.
Розповсюдження ключів ред.
Для того, щоб Боб міг відправити свої секретні повідомлення, Аліса передає свій відкритий ключ (n, e) Бобу через надійний, але не обов'язково секретний маршрут. Секретний ключ d ніколи не розповсюджується.
Генерація ключів ред.
Для того, щоб згенерувати пари ключів виконуються такі дії:
- Вибираються два великі прості числа і приблизно 512 біт завдовжки кожне
- Обчислюється їх добуток
- Обчислюється функція Ейлера
- Вибирається ціле число таке, що та взаємно просте з
- За допомогою розширеного алгоритму Евкліда знаходиться число таке, що
Число називається модулем, а числа і — відкритою й секретною експонентами (англ. encryption and decryption exponents), відповідно. Пари чисел є відкритою частиною ключа, а — секретною. Числа і після генерації пари ключів можуть бути знищені, але в жодному разі не повинні бути розкриті.
Шифрування ред.
Припустимо, що Боб хотів би відправити повідомлення M Алісі. Спочатку він перетворює M в ціле число m так, щоб 0 ≤ m < n за допомогою узгодженого оборотного протоколу, відомого як схеми доповнення. Потім він обчислює зашифрований текст c, використовуючи відкритий ключ Аліси e, за допомогою рівняння:
- .
Це може бути зроблено досить швидко, навіть для 500-бітних чисел, з використанням модульного зведення в ступінь. Потім Боб передає c Алісі.
Розшифрування ред.
Для розшифрування повідомлення Боба m Алісі потрібно обчислити таку рівність:
- .
Неважко переконатися, що при розшифруванні відновиться вихідне повідомлення:
З умови
випливає, що
- для деякого цілого , отже
Згідно з теоремою Ейлера:
- ,
тому
RSA припущення — RSA є односторонньою перестановкою, тобто для будь-якого дієвого алгоритму A ймовірність
- дуже мала, що означає неможливість обернення RSA без секретної інформації — .
Наведений вище варіант шифрування називається RSA з підручника (англ. textbook RSA)[1] і є цілком уразливим. В жодному разі його не можна використовувати в криптосистемах.
Приклад ред.
| Етап | Опис операції | Результат операції |
|---|---|---|
| Генерація ключів | Обрати два простих різних числа |
|
| Обчислити добуток |
| |
| Обчислити функцію Ейлера |
| |
| Обрати відкриту експоненту |
| |
| Обчислити секретну експоненту |
| |
| Опублікувати відкритий ключ |
| |
| Зберегти секретний ключ |
| |
| Шифрування | Обрати текст для шифрування |
|
| Обчислити шифротекст |
| |
| Розшифрування | Обчислити вихідне повідомлення |
|
Цифровий підпис ред.
RSA може використовуватися не тільки для шифрування, але й для цифрового підпису. Підпис повідомлення обчислюється з використанням секретного ключа за формулою:
Для перевірки правильності підпису потрібно переконатися, що виконується рівність:
Деякі особливості алгоритму ред.
Генерація простих чисел ред.
Для знаходження двох великих простих чисел і , при генерації ключа, звичайно використовуються ймовірнісні тести чисел на простоту, які дозволяють швидко виявити й відкинути складені числа.
Для генерації і необхідно використовувати криптографічно надійний генератор випадкових чисел. У порушника не має бути можливості одержати будь-яку інформацію про значення цих чисел.
і не повинні бути занадто близькими одне до одного, інакше можна буде знайти їх використовуючи метод факторизації Ферма. Крім того, необхідно вибирати «сильні» прості числа, щоб не можна було скористатися p-1 алгоритмом Поларда.
Доповнення повідомлень ред.
При практичному використанні необхідно деяким чином доповнювати повідомлення. Відсутність доповнень може призвести до деяких проблем:
- значення і дадуть при шифруванні шифротексти 0 і 1 при будь-яких значеннях і .
- при малому значенні відкритого показника ( , наприклад) можлива ситуація, коли виявиться, що . Тоді , і зловмисник легко зможе відновити вихідне повідомлення, обчисливши корінь ступеня з .
- оскільки RSA є детермінованим алгоритмом, тобто не використовує випадкових значень у процесі роботи, то зловмисник може використати атаку з обраним відкритим текстом.
Для розв'язання цих проблем повідомлення доповнюються, перед кожним шифруванням, деяким випадковим значенням. Доповнення виконується таким чином, щоб гарантувати, що , і . Крім того, оскільки повідомлення доповнюється випадковими даними, то шифровуючи той самий відкритий текст, ми щораз будемо одержувати інше значення шифротексту, що робить атаку з обраним відкритим текстом неможливою.
Вибір значення відкритого показника ред.
RSA працює значно повільніше симетричних алгоритмів. Для підвищення швидкості шифрування відкритий показник вибирається невеликим, звичайно 3, 17 або 65537 (2 обрати не можна, бо повинно бути взаємно простим із ). Ці числа у двійковому вигляді містять тільки по дві одиниці, що зменшує число необхідних операцій множення при піднесенні до степеня. Наприклад, для піднесення числа до степеня 17 потрібно виконати тільки 5 операцій множення:
Вибір малого значення відкритого показника може призвести до розкриття повідомлення, якщо воно відправляється відразу декільком одержувачам, але ця проблема вирішується за рахунок доповнення повідомлень.
Вибір значення секретного показника ред.
Значення секретного показника повинне бути досить великим. У 1990 році Міхаель Вінер (Michael J. Wiener) показав, що якщо і , то є ефективний спосіб обчислити по і . Однак, якщо значення вибирається невеликим, то виявляється досить великим і проблеми не виникає.
Довжина ключа ред.
Число n повинне мати розмір не менше 512 біт. На 2007 рік система шифрування на основі RSA вважалась надійною, починаючи з величини N в 1024 біти.
Проблеми реалізації ред.
ROCA ред.
В жовтні 2017 року міжнародна група дослідників (Словаччина, Чехія, Велика Британія, Італія) оприлюднили доповідь про виявлену ними вразливість в алгоритмі генератора псевдовипадкових чисел в криптографічній бібліотеці компанії Infeneon. Дана вразливість виникає при роботі бібліотеки на смарт-картах та в подібних вбудованих системах. Виявлені вади роблять практично досяжною факторизацію використаних при генерації пари ключів простих чисел. Зловмисник має можливість відновити секретний ключ за відкритим ключем жертви[2][3].
Станом на 2017 рік дослідники оцінюють витрати у найгіршому випадку для атаки методом Коперсміта проти ключа розміром 2048-біт 17 днів за $40 300 та $76 за 45 хвилин для ключа розміром 1024-біт (для орендованого кластера з тисячі вузлів на Amazon Web Service). В середньому витрати будуть вдвічі менші. При цьому, ключ розміром 4096 біт виявився слабшим за ключ розміром 3072 біт, для якого атака лишається практично важкою[2].
Дослідники також створили алгоритм для перевірки ключа на вразливість до виявленої ними атаки. Перевірка потребує близько 1 мілісекунди на сучасному процесорі[2].
Вразливі ключі були виявлені у низці продуктів та інтернет-проектах. В тому числі, було виявлено понад 750 000 вразливих до атаки смарт-карт системи електронного громадянства Естонії, ключах Yubikey 4, тощо[2]. 1 листопада 2017 року Естонія розпочала процес оновлення цифрових посвідчень з переходом на використання алгоритмів криптографії на еліптичних кривих[4].
Вражена бібліотека пройшла сертифікацію NIST FIPS 140-2 Level 2 та Common Criteria, а вразливість була присутня в ній з 2012 року[2].
Виявлена вада отримала назву ROCA та код CVE-2017-15361[5].
Див. також ред.
Примітки ред.
- ↑ The RSA one way permutation Textbook RSA is insecure [Архівовано 30 листопада 2012 у Wayback Machine.] на сайті Стенфордського університету (англ.)
- ↑ а б в г д Dan Goodin (Oct 16 2017). Millions of high-security crypto keys crippled by newly discovered flaw. Ars Technica. Архів оригіналу за 19 жовтня 2018. Процитовано 17 квітня 2021.
- ↑ Matus Nemec, Marek Sys, Petr Svenda, Dusan Klinec, Vashek Matyas (2017). The Return of Coppersmith's Attack: Practical Factorization of Widely Used RSA Moduli. 24th ACM Conference on Computer and Communications Security (CCS'2017). ACM: 1631—1648. doi:10.1145/3133956.3133969. ISBN 978-1-4503-4946-8.
- ↑ Kaspar Korjus (30 жовтня 2017). Estonia is enhancing the security of its digital identities. Архів оригіналу за 4 травня 2021. Процитовано 17 квітня 2021.
- ↑ ROCA: Vulnerable RSA generation (CVE-2017-15361). CRoCS Wiki. Архів оригіналу за 23 березня 2021. Процитовано 19 жовтня 2017.
Література ред.
- Menezes A. J., van Oorschot P. C., Vanstone S. A. Handbook of Applied Cryptography. — CRC Press, 1996. — 794 p. (pdf [Архівовано 20 квітня 2015 у Wayback Machine.])
- Брассар Ж. Современная криптология = Modern Cryptology: A Tutorial. — М. : Полимед, 1999. — 176 с.
- Земор Ж. Курс криптографии = Cours de cryptographie. — Ижевск : РХД, 2006. — 256 с.
- Коутинхо С. Введение в теорию чисел. Алгоритм RSA = The Mathematics of Ciphers: Number Theory and RSA Cryptography. — М. : Постмаркет, 2001. — 328 с.
- ван Тилборг Х. К. А. Основы криптологии = Fundamentals of Cryptology. — М. : Мир, 2006. — 472 с.
- Ян С. Криптоанализ RSA = Cryptanalytic Attacks on RSA. — Ижевск : РХД, 2011. — 312 с.
- Ященко В. В. Введение в криптографию. — М. : МЦНМО, 2012. — 348 с. (pdf [Архівовано 20 березня 2014 у Wayback Machine.])
| Це незавершена стаття з криптографії. Ви можете допомогти проєкту, виправивши або дописавши її. |
| Ця стаття потребує додаткових посилань на джерела для поліпшення її перевірності. (січень 2017) |